Knowledge Check consistent dependent, consistent independent; or “incor For each System Of linear equations shown below, classify the system as best description of its solution. The system has exactly one solution; The system has no solution. System System A: Line A: y = 3x Line B: y = x + 3 System B: Line A: y = 2x – 2 Line B: y = x – 1 System C: Line A: y = mx Line B: y = x – 1 This means the system has: infinitely many solutions This means the system has: unique solution This means the system has: no solution
The Correct Answer and Explanation is:
Here is the correct analysis and solution for each system of linear equations.
Understanding Systems of Linear Equations
A system of linear equations consists of two or more linear equations. The solution to a system is the point (or points) that satisfy all equations in the system simultaneously. Graphically, this corresponds to the intersection point(s) of the lines. We can classify systems into three categories:
- Consistent Independent: The lines have different slopes and intersect at exactly one point. This system has one unique solution.
- Inconsistent: The lines have the same slope but different y-intercepts. They are parallel and never intersect. This system has no solution.
- Consistent Dependent: The equations represent the same line (same slope and same y-intercept). The lines overlap at every point. This system has infinitely many solutions.
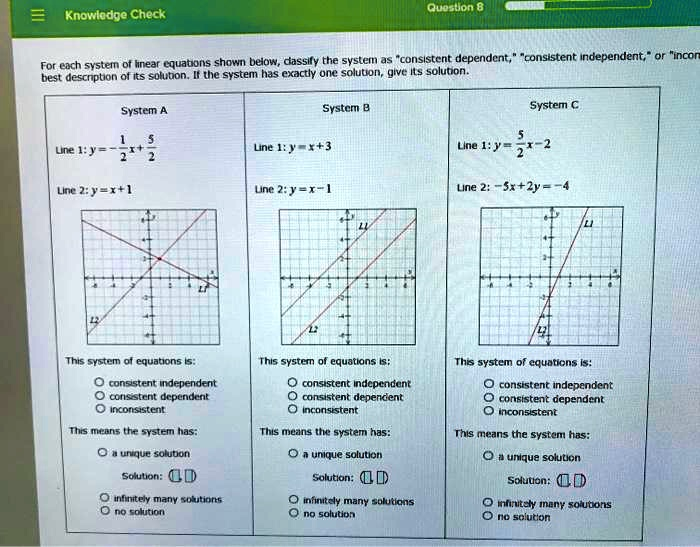
System A
- Equations:
- Line 1: y = -½x + ⁵/₂
- Line 2: y = x + 1
- Analysis: The slope of Line 1 is -½, and the slope of Line 2 is 1. Since the slopes are different, the lines must intersect at exactly one point.
- Conclusion:
- This system of equations is: consistent independent.
- This means the system has: a unique solution.
- Solution: By examining the graph, the lines intersect at the point (1, 2). We can verify this algebraically by setting the equations equal:
-½x + ⁵/₂ = x + 1
-x + 5 = 2x + 2
3 = 3x
x = 1
Substituting x=1 into the second equation gives y = 1 + 1 = 2.
The solution is (1, 2).
System B
- Equations:
- Line 1: y = x + 3
- Line 2: y = x – 1
- Analysis: The slope of Line 1 is 1, and the slope of Line 2 is also 1. The y-intercept of Line 1 is 3, while the y-intercept of Line 2 is -1. Since the slopes are the same but the y-intercepts are different, the lines are parallel and will never intersect.
- Conclusion:
- This system of equations is: inconsistent.
- This means the system has: no solution.
System C
- Equations:
- Line 1: y = ⁵/₂x – 2
- Line 2: -5x + 2y = -4
- Analysis: To compare these equations, let’s rewrite Line 2 in slope-intercept form (y = mx + b):
-5x + 2y = -4
2y = 5x – 4
y = ⁵/₂x – 2
Now, comparing the two equations, we see they are identical. Both have a slope of ⁵/₂ and a y-intercept of -2. This means they are the same line. - Conclusion:
- This system of equations is: consistent dependent.
- This means the system has: infinitely many solutions, as every point on the line is a solution to the system.
