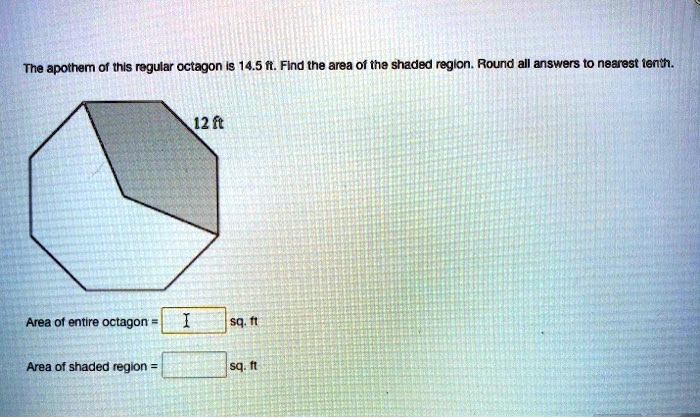
shaded region. Round all answers to the nearest tenth. 12 ft Area of entire octagon Area of shaded region
The apothem of this regular octagon is 14.5 ft. Find the area of the shaded region. Round all answers to the nearest tenth. 12 ft Area of entire octagon Area of shaded region
The Correct Answer and Explanation is:
Answer:
Area of entire octagon = 696.0 sq. ft
Area of shaded region = 261.0 sq. ft
Explanation:
This problem requires finding the area of a regular octagon and a specific shaded portion of it. The solution can be found by following a systematic, step-by-step process.
1. Identify Given Information and Key Formulas
First, identify the known values from the problem statement and the diagram:
- The polygon is a regular octagon, which means it has 8 equal sides and 8 equal interior angles.
- The number of sides (n) = 8.
- The length of one side (s) = 12 ft.
- The length of the apothem (a) = 14.5 ft. The apothem is the perpendicular distance from the center of the polygon to the midpoint of a side.
The formula for the area of any regular polygon is:
Area = ½ × apothem × perimeter
or
Area = ½ * a * P
2. Calculate the Perimeter of the Octagon
The perimeter (P) of a polygon is the sum of the lengths of all its sides. Since this is a regular octagon with 8 sides of equal length:
P = n × s
P = 8 × 12 ft
P = 96 ft
3. Calculate the Area of the Entire Octagon
Now, use the area formula with the known apothem and the calculated perimeter:
Area = ½ * a * P
Area = ½ × 14.5 ft × 96 ft
Area = 0.5 × 14.5 × 96
Area = 696 sq. ft
Rounding to the nearest tenth, the area of the entire octagon is 696.0 sq. ft.
4. Calculate the Area of the Shaded Region
A regular octagon can be divided into 8 congruent (identical) isosceles triangles, with their vertices meeting at the center. The shaded region in the diagram is composed of 3 of these 8 identical triangles.
Therefore, the area of the shaded region is 3/8 of the total area of the octagon.
Area of shaded region = (3/8) × Area of entire octagon
Area of shaded region = (3/8) × 696 sq. ft
Area of shaded region = 0.375 × 696 sq. ft
Area of shaded region = 261 sq. ft
Rounding to the nearest tenth, the area of the shaded region is 261.0 sq. ft.
