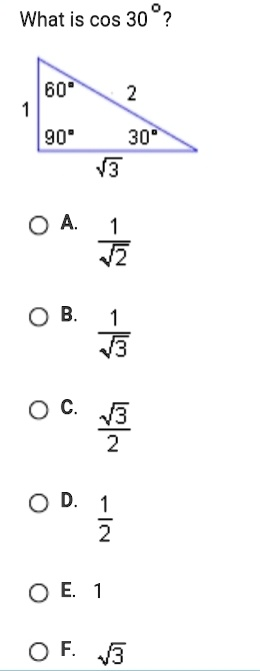
What is cos 30°? 60° 2 1 90° 30° ?3 A.
B.
The Correct Answer and Explanation is:
C. √3 / 2
Explanation:
To determine the value of cos 30°, we can use the principles of trigonometry as applied to a right-angled triangle. The mnemonic SOH CAH TOA is a helpful tool for remembering the trigonometric ratios:
- SOH: Sine = Opposite / Hypotenuse
- CAH: Cosine = Adjacent / Hypotenuse
- TOA: Tangent = Opposite / Adjacent
The problem provides a 30-60-90 right-angled triangle with its side lengths clearly labeled. To find the cosine of the 30° angle, we must first identify the sides of the triangle relative to this specific angle.
- Hypotenuse: This is always the longest side of a right-angled triangle and is directly opposite the 90° angle. In the given triangle, the hypotenuse has a length of 2.
- Adjacent Side: This is the side that is next to the 30° angle, but is not the hypotenuse. For the 30° angle, the adjacent side has a length of √3.
- Opposite Side: This is the side directly across from the 30° angle. In this case, the opposite side has a length of 1.
Now, we apply the “CAH” formula for cosine:
Cosine = Adjacent / Hypotenuse
Substituting the values we identified from the triangle:
cos 30° = (Length of Adjacent Side) / (Length of Hypotenuse)
cos 30° = √3 / 2
Therefore, the value of cos 30° is √3 / 2. This corresponds to option C. This is a fundamental value in trigonometry, derived from the properties of a 30-60-90 special right triangle.
