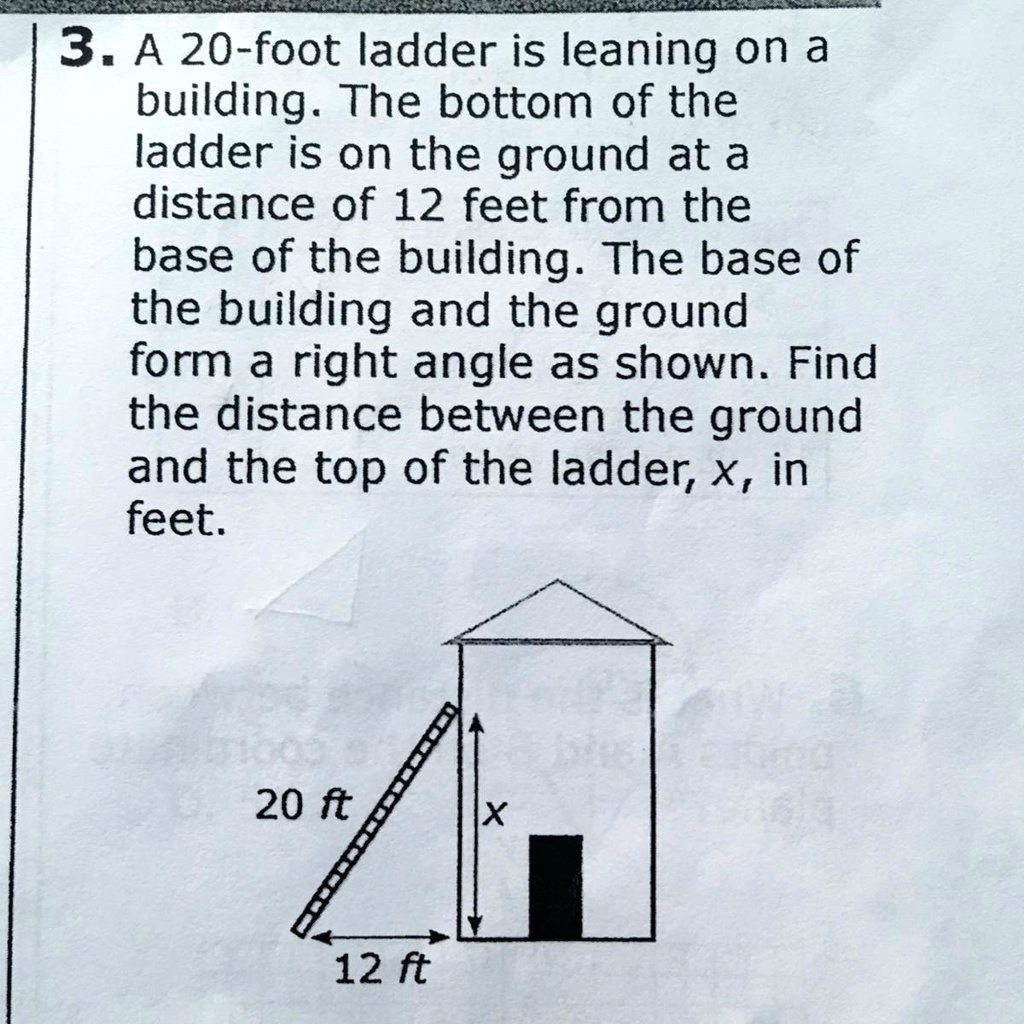
A 20-foot ladder is leaning on a building. The bottom of the ladder is on the ground at a distance of 12 feet from the base of the building. The base of the building and the ground form a right angle as shown. Find the distance between the ground and the top of the ladder, x, in feet
The Correct Answer and Explanation is:
To find the distance between the ground and the top of the ladder, labeled as xxx, the Pythagorean Theorem offers a direct solution. In this problem, the ladder forms the hypotenuse of a right triangle, while the distance from the building (12 feet) and the vertical height from the ground to the top of the ladder (xxx) form the two legs.
The Pythagorean Theorem states:a2+b2=c2a^2 + b^2 = c^2a2+b2=c2
Here:
- a=12a = 12a=12 feet (horizontal distance),
- b=xb = xb=x feet (vertical height),
- c=20c = 20c=20 feet (length of the ladder).
Substitute the known values:122+x2=20212^2 + x^2 = 20^2122+x2=202144+x2=400144 + x^2 = 400144+x2=400×2=400−144=256x^2 = 400 – 144 = 256×2=400−144=256x=256=16x = \sqrt{256} = 16x=256=16
Answer: x=16x = 16x=16 feet.
Explanation
This problem involves a classic application of the Pythagorean Theorem, which applies to right triangles. A ladder leaning against a building naturally creates a right triangle, where the ground and the building form the two perpendicular sides. The ladder, inclined from the ground to the building, serves as the hypotenuse.
Understanding the relationship between the sides of a right triangle is essential. According to the Pythagorean Theorem, the square of the hypotenuse equals the sum of the squares of the other two sides. In this scenario, the hypotenuse measures 20 feet (the ladder), and one leg of the triangle (the distance from the building to the bottom of the ladder) is 12 feet.
By plugging in the values into the Pythagorean Theorem formula, squaring the known sides, and isolating the unknown side (xxx), the missing height can be determined algebraically. Subtracting the square of the horizontal leg from the square of the hypotenuse gives the square of the vertical leg. Taking the square root of that result provides the final answer.
This problem not only reinforces understanding of geometric principles but also highlights the importance of precise calculation and logical progression through algebraic steps. Real-world applications of this concept appear frequently in construction, engineering, and design, where determining the length or height in angled structures is necessary for safety and accuracy. Understanding this type of problem helps build critical problem-solving skills.
