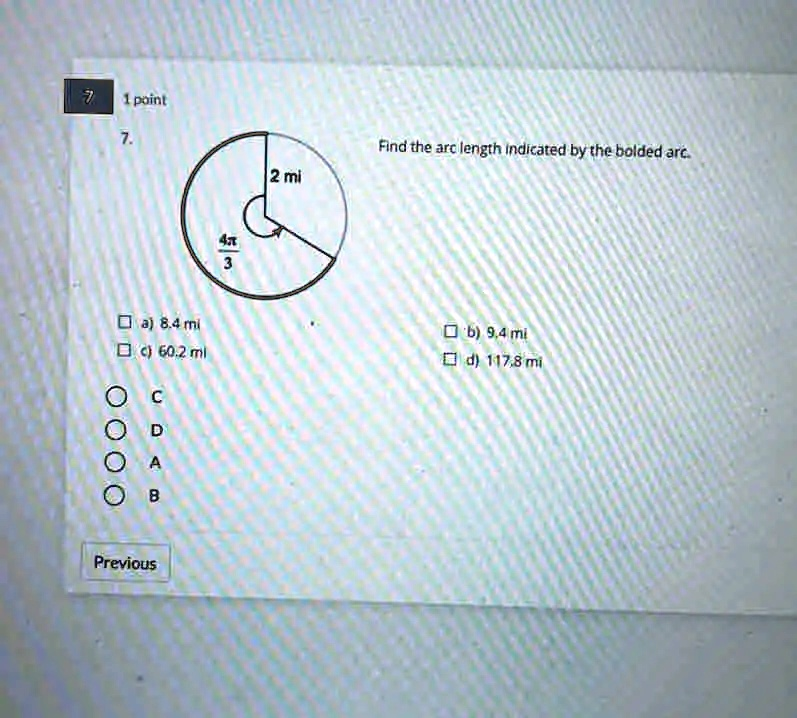
Find the arc length indicated by the bolded arc 2 mi 0 J) 8.4 mi D € 60.2 mi D’b) 9.4 mi 0 d 117.8 mi D A 8 Previous
The Correct Answer and Explanation is:
Correct Answer: a) 8.4 mi
Explanation:
This problem requires us to find the length of a specific arc of a circle. The arc length is the distance along the curved line that makes up the arc.
1. Identify Given Information:
From the provided image, we can identify two key pieces of information:
- Radius (r): The radius of the circle is given as 2 mi.
- Central Angle (θ): The angle that subtends the bolded arc is given in radians as 4π/3.
2. Select the Appropriate Formula:
The formula for calculating the arc length (s) of a circle depends on the unit of the central angle. When the central angle (θ) is given in radians, the formula is:
s = r * θ
Where:
- s is the arc length.
- r is the radius of the circle.
- θ is the central angle in radians.
This formula is a direct and efficient way to find the arc length because the definition of a radian is based on the ratio of arc length to the radius.
3. Substitute Values and Calculate:
Now, we substitute the given values into the formula:
- r = 2 mi
- θ = 4π/3
s = 2 * (4π/3)
s = 8π / 3 mi
This is the exact arc length in terms of π. To find the numerical value that matches the multiple-choice options, we will use the approximation for π ≈ 3.14159.
s ≈ (8 * 3.14159) / 3
s ≈ 25.13272 / 3
s ≈ 8.37757 mi
4. Compare and Conclude:
The calculated arc length is approximately 8.37757 mi. We now compare this value to the given options:
- a) 8.4 mi
- b) 9.4 mi
- c) 60.2 mi
- d) 117.8 mi
Our calculated value, when rounded to one decimal place, is 8.4 mi. This matches option (a).
Therefore, the length of the bolded arc is 8.4 mi.thumb_upthumb_down
