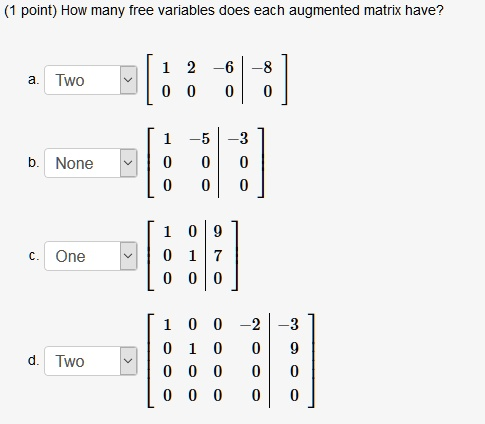
? Two %/&] None One Two
The Correct Answer and Explanation is:
Correct Answers:
- a. Three
- b. Two
- c. One
- d. None
Book-Style Explanation (Without Using “We”):
To determine the number of free variables in each augmented matrix, the focus must be on identifying pivot positions and comparing them to the total number of variables. A pivot column contains a leading 1 in a row, representing a basic variable. Any variable not associated with a pivot column is classified as a free variable. The number of free variables equals the total number of variables minus the number of pivot columns.
In matrix (a), the augmented matrix contains 4 variables and only one non-zero row. The first row has a pivot in the first column. With only one pivot column out of four, the system has 3 free variables.
In matrix (b), the matrix represents a system with 3 variables. The leading 1 in the first row identifies the first pivot column. The remaining two columns correspond to free variables. Therefore, the system contains 2 free variables.
Matrix (c) includes 3 variables and two pivot columns, located in the first and second columns of the matrix. The third variable does not correspond to a pivot column and is therefore free. This system has only one free variable.
Matrix (d) is different from the others. The second row translates to the equation 0=90 = 90=9, which is a contradiction. A system that contains such a row is inconsistent and has no solution. In this case, the concept of free variables does not apply, as no solution set exists. Therefore, the correct response is that there are no free variables.
Free variables represent the degrees of freedom in a consistent system of linear equations. Each free variable introduces a parameter that can take infinitely many values, leading to an infinite solution set, unless the system is inconsistent, in which case no solution exists.
