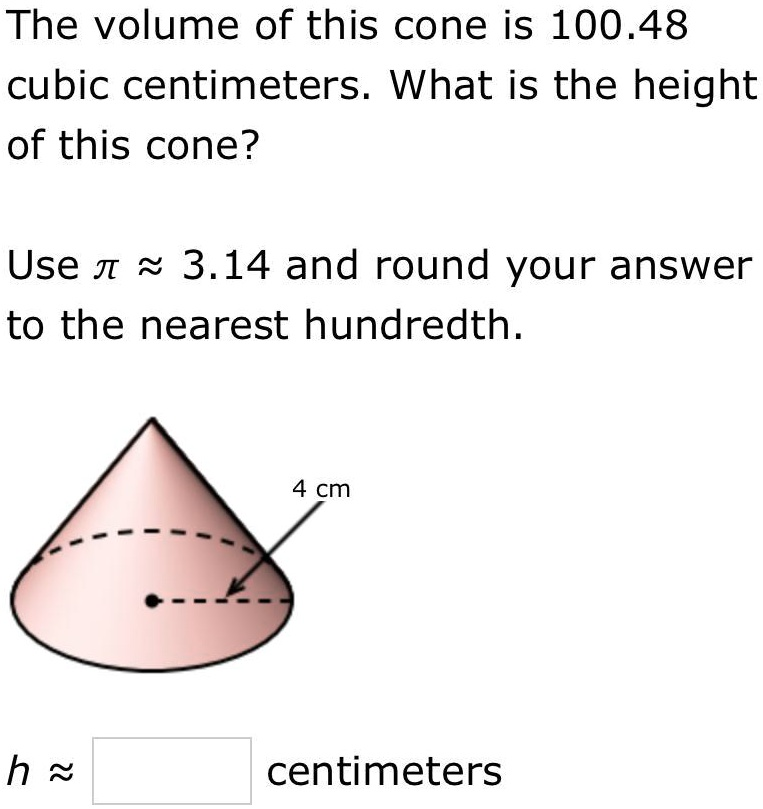
The volume of this cone is 100.48 cubic centimeters. What is the height of this cone? Use
and round your answer to the nearest hundredth. 4 cm h
centimeters
The Correct Answer and Explanation is:
To find the height of the cone, one must use the formula for the volume of a cone: V = (1/3)πr²h. In this formula, V stands for volume, π (pi) is a mathematical constant, r represents the radius of the circular base, and h is the height of the cone.
The problem provides the following values:
- The volume (V) is 100.48 cubic centimeters.
- The radius (r) of the cone’s base is 4 centimeters.
- The value to use for π is approximately 3.14.
The unknown variable to solve for is the height (h). The first step is to substitute the given values into the volume formula:
100.48 = (1/3) × 3.14 × (4)² × h
Next, proceed with simplifying the equation. Start by calculating the square of the radius (r²):
4² = 4 × 4 = 16
Now, substitute this value back into the equation:
100.48 = (1/3) × 3.14 × 16 × h
Then, multiply the numerical values on the right side of the equation:
3.14 × 16 = 50.24
The equation now looks like this:
100.48 = (1/3) × 50.24 × h
To solve for h, it’s necessary to isolate it. Begin by eliminating the fraction (1/3). This is done by multiplying both sides of the equation by 3:
3 × 100.48 = 3 × [(1/3) × 50.24 × h]
301.44 = 50.24 × h
The final step to find h is to divide both sides of the equation by 50.24:
h = 301.44 / 50.24
Performing the division results in:
h = 6
The problem asks for the answer to be rounded to the nearest hundredth. Since the calculated height is exactly 6, it can be written as 6.00 to meet this requirement.
Thus, the height of the cone is approximately 6.00 centimeters.
