10 y 9 8 7 6 5 4 3 2 1 x -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8 9 10 -1 -2 -3 -4 -5 -6 -7 -8 -9 -10
The Correct Answer and Explanation is:
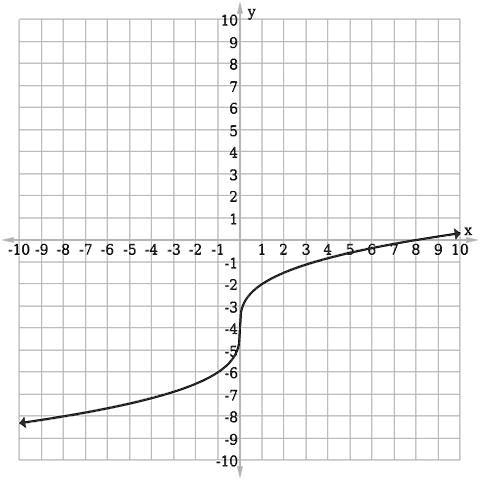
The graph in the image represents a sigmoid function, typically expressed as:
f(x)=11+e−xf(x) = \frac{1}{1 + e^{-x}}
This function exhibits an S-shaped curve, where values transition smoothly from lower to higher y-values. The key characteristics include:
- Domain: All real numbers (−∞,∞-\infty, \infty).
- Range: Values constrained between 00 and 11.
- Asymptotes: The function approaches 00 as x→−∞x \to -\infty and 11 as x→∞x \to \infty.
- Inflection Point: Located at x=0x = 0, where the most rapid change occurs.
Explanation
The sigmoid function is crucial in mathematical modeling, particularly in probability and machine learning. Its smooth transition from one state to another makes it ideal for logistic regression, where outcomes are binary. The shape arises from the exponential term e−xe^{-x}, controlling the steepness of the curve.
At large negative values of xx, the denominator increases, driving f(x)f(x) toward zero. In contrast, large positive values make the denominator approach 11, pushing f(x)f(x) toward unity. This makes the function useful for neural networks, transforming inputs into values suitable for decision boundaries.
In physics, applications include modeling growth rates or chemical reactions with saturation limits. Biology leverages it for population studies, predicting how species adapt to resource availability. Digital signal processing also benefits from its smooth transition, preventing abrupt changes in data output.
From a geometric perspective, the function’s concavity shifts at x=0x = 0, marking a critical point in its behavior. The symmetry about this point aligns with properties seen in natural systems, making it relevant across various domains.
This visualization aids comprehension by illustrating gradual transformations rather than abrupt transitions, reflecting real-world phenomena with continuity and precision. Understanding the sigmoid curve fosters insights into numerous scientific applications.
