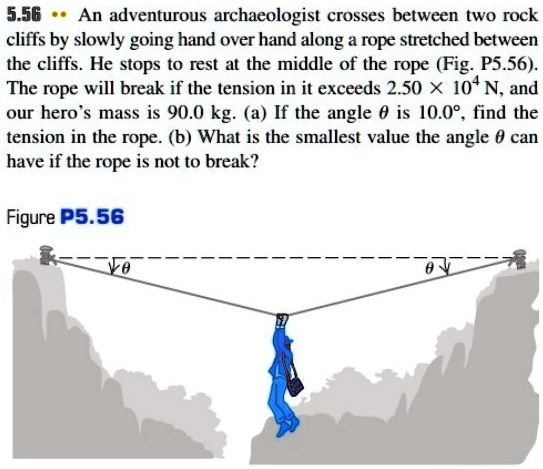
An adventurous archaeologist crosses between two rock cliffs by slowly going hand over hand along rope stretched between the cliffs. He stops to rest at the middle of the rope (Fig: P5.56). The rope will break if the tension in it exceeds 2.50 X 104N, and our hero’$ mass is 90.0 kg: (a) If the angle 0 is 10.09 . find the tension in the rope. (b) What is the smallest value the angle 0 can have if the rope is not t0 break? Figure P5.56
The Correct Answer and Explanation is:
Given:
- Mass of the archaeologist: m=90.0 kgm = 90.0 \, \text{kg}m=90.0kg
- Gravitational acceleration: g=9.8 m/s2g = 9.8 \, \text{m/s}^2g=9.8m/s2
- Weight: W=mg=90.0×9.8=882 NW = mg = 90.0 \times 9.8 = 882 \, \text{N}W=mg=90.0×9.8=882N
- Maximum tension: Tmax=2.50×104 NT_{\text{max}} = 2.50 \times 10^4 \, \text{N}Tmax=2.50×104N
- He is at the midpoint → rope is symmetric
- The vertical component of the tension supports the weight.
- θ\thetaθ: angle between rope and horizontal.
(a) Find tension when θ=10.0∘\theta = 10.0^\circθ=10.0∘
Since the system is symmetric, the vertical components of the tension in the two rope segments must add up to balance the weight: 2Tsin(θ)=mg2T \sin(\theta) = mg2Tsin(θ)=mg T=mg2sin(θ)T = \frac{mg}{2 \sin(\theta)}T=2sin(θ)mg
Substitute known values: T=8822sin(10∘)=8822×0.1736=8820.3472≈2541 NT = \frac{882}{2 \sin(10^\circ)} = \frac{882}{2 \times 0.1736} = \frac{882}{0.3472} \approx 2541 \, \text{N}T=2sin(10∘)882=2×0.1736882=0.3472882≈2541N
✅ Answer (a): The tension is approximately 2541 N when the angle is 10∘10^\circ10∘.
(b) What is the smallest angle θ\thetaθ so the rope does not break?
We solve for θ\thetaθ in the formula: T=mg2sin(θ)≤2.50×104T = \frac{mg}{2 \sin(\theta)} \leq 2.50 \times 10^4T=2sin(θ)mg≤2.50×104 sin(θ)≥mg2×2.50×104=88250000=0.01764\sin(\theta) \geq \frac{mg}{2 \times 2.50 \times 10^4} = \frac{882}{50000} = 0.01764sin(θ)≥2×2.50×104mg=50000882=0.01764 θ≥sin−1(0.01764)≈1.01∘\theta \geq \sin^{-1}(0.01764) \approx 1.01^\circθ≥sin−1(0.01764)≈1.01∘
✅ Answer (b): The smallest angle θ\thetaθ can have is approximately 1.01° to prevent the rope from breaking.
