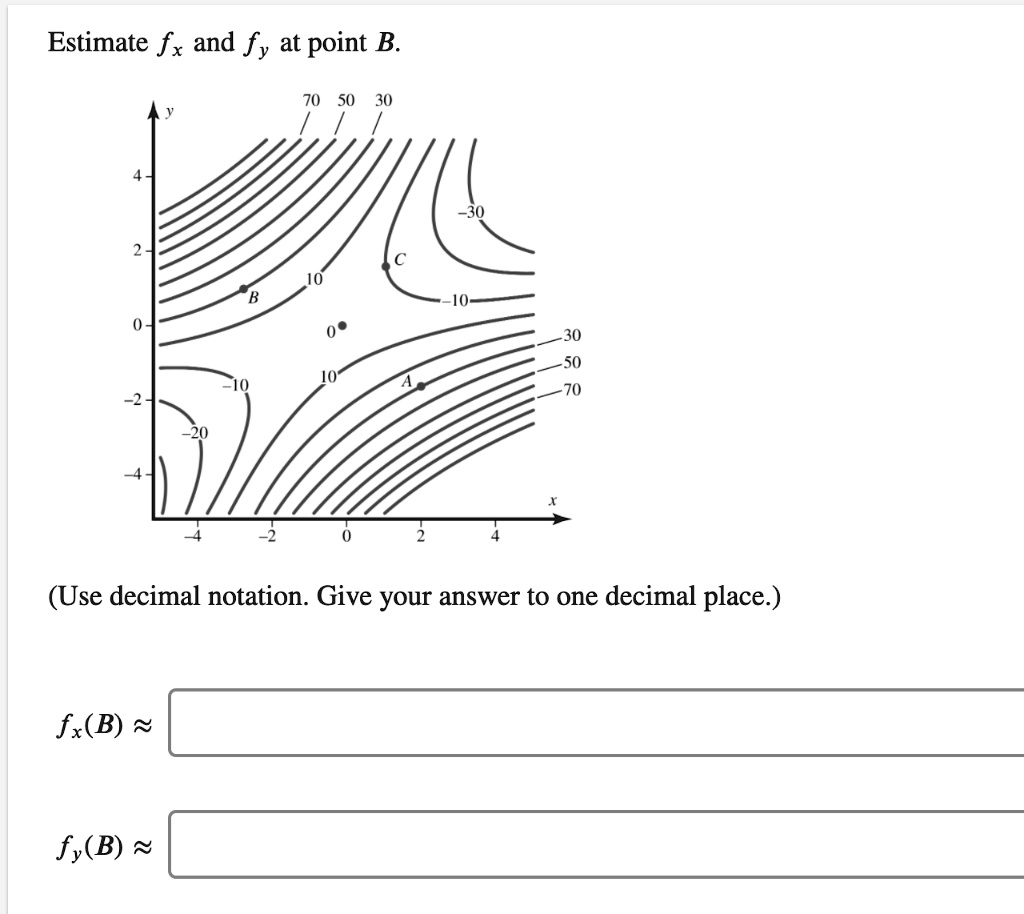
The Correct Answer and Explanation is:
The estimated partial derivatives at point B are:
fx(B) ≈ 2.5
fy(B) ≈ -10
Explanation
Partial derivatives represent the rate of change of a function with respect to one variable while holding the other variable constant. In this case, fx measures the rate of change of f with respect to x while fy measures the rate of change with respect to y.
To estimate fx at point B, we analyze the contour lines in the region surrounding B. Point B is located between the contour lines labeled 0 and 10. Moving in the positive x-direction from B, the function value increases from 0 to 10 over a horizontal distance of approximately 4 units. The rate of change is found by dividing the change in function value by the change in x:
fx(B) ≈ (10 – 0) / (2 – (-2)) = 10 / 4 = 2.5
Next, to estimate fy at point B, we examine the function’s variation along the y-axis. Point B is situated between the contour lines labeled 0 and -10. Moving vertically upward, the function value decreases from 0 to -10 over a vertical distance of approximately 1 unit. The rate of change in the function due to a change in y is:
fy(B) ≈ (-10 – 0) / (1 – 0) = -10 / 1 = -10
These derivatives indicate how the function changes near point B. A positive fx suggests an increase in function value as x increases, while a negative fy signifies a decrease as y increases. This information can be useful in understanding the local behavior of f(x, y) and how it varies across the coordinate plane.
