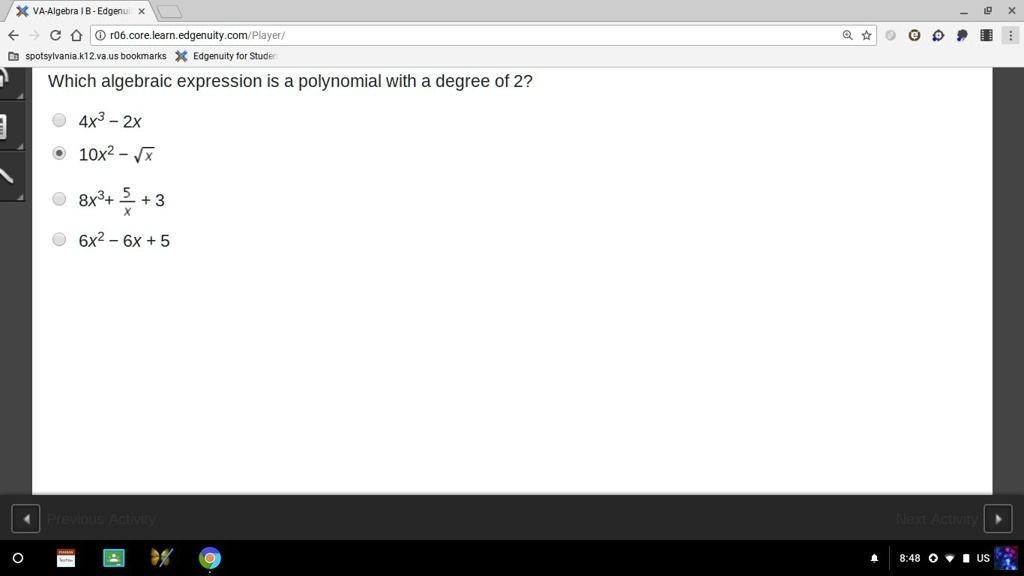
Which algebraic expression is a polynomial with a degree of 2? 4x³ – 2x 10x² – ?x 8x³ + \frac{5}{x} + 3 6x² – 6x + 5
The Correct Answer and Explanation is:
The correct answer is 6x² – 6x + 5.
To determine the correct answer, we must first understand the two conditions given in the question. The algebraic expression must be a polynomial, and it must have a degree of 2.
First, let’s define what makes an expression a polynomial. A polynomial is an algebraic expression that consists of variables, coefficients, and constants, using only addition, subtraction, and multiplication. A key rule for polynomials is that the exponents of the variables must be non-negative integers (0, 1, 2, 3, and so on). This means that expressions with variables in the denominator (which corresponds to a negative exponent) or variables under a radical sign (which corresponds to a fractional exponent) are not polynomials.
Second, the degree of a polynomial is the value of the highest exponent of the variable in the expression.
Now let’s analyze each option:
- 4x³ – 2x: This expression is a polynomial because the exponents of the variable x are 3 and 1, which are non-negative integers. However, the highest exponent is 3, so its degree is 3, not 2.
- 10x² – √x: This expression is not a polynomial. The term √x is equivalent to x^(1/2). Since the exponent 1/2 is a fraction and not a non-negative integer, the entire expression does not qualify as a polynomial.
- 8x³ + 5/x + 3: This expression is also not a polynomial. The term 5/x is equivalent to 5x^(-1). Since the exponent -1 is negative, the expression fails the definition of a polynomial.
- 6x² – 6x + 5: This expression is a polynomial. The terms are 6x², –6x (which is –6x¹), and a constant, 5. The exponents on the variable x are 2 and 1, both of which are non-negative integers. The highest exponent in the expression is 2. Therefore, this is a polynomial with a degree of 2.
