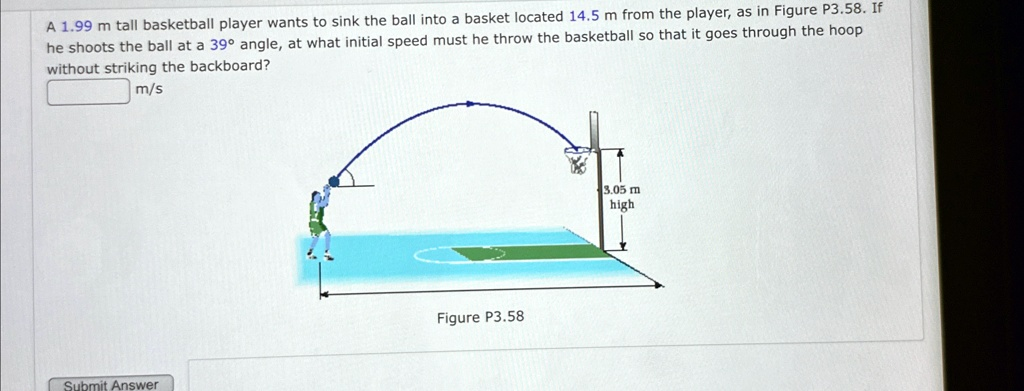
A 1.99 m tall basketball player wants to sink the ball into a basket located 14.5 m from the player, as in Figure P3.58. If he shoots the ball at a
angle, at what initial speed must he throw the basketball so that it goes through the hoop without striking the backboard
The Correct Answer and Explanation is:
12.64
To find the initial speed of the basketball, we can analyze its motion using the principles of projectile motion. We will break the motion down into its horizontal and vertical components.
First, let’s establish a coordinate system and list the known variables. Let the point where the ball is released be the origin (0,0) for simplicity in the initial calculation, and then adjust for the height difference. An alternative and more direct approach is to set the origin at the player’s feet. Let’s use the latter.
Known Information:
- Initial horizontal position (x₀) = 0 m
- Initial vertical position (y₀) = 1.99 m (the height of the player)
- Final horizontal position (x) = 14.5 m (the distance to the basket)
- Final vertical position (y) = 3.05 m (the height of the basket)
- Launch angle (θ) = 39°
- Acceleration due to gravity (g) = 9.8 m/s² (acting downwards)
Equations of Motion:
The motion of the basketball can be described by two kinematic equations, where v₀ is the initial speed we need to find:
- Horizontal motion (constant velocity):
x = x₀ + (v₀ cosθ)t => 14.5 = 0 + (v₀ cos(39°))t - Vertical motion (constant acceleration):
y = y₀ + (v₀ sinθ)t – (1/2)gt² => 3.05 = 1.99 + (v₀ sin(39°))t – (1/2)(9.8)t²
We have a system of two equations with two unknowns: the initial speed (v₀) and the time of flight (t). We can solve this by first isolating ‘t’ in the horizontal equation:
t = 14.5 / (v₀ cos(39°))
Next, we substitute this expression for ‘t’ into the vertical equation. This eliminates ‘t’ and leaves us with an equation containing only v₀:
3.05 = 1.99 + (v₀ sin(39°)) * [14.5 / (v₀ cos(39°))] – 4.9 * [14.5 / (v₀ cos(39°))]²
Let’s simplify this equation. The v₀ terms cancel in the middle term, and sin(39°)/cos(39°) becomes tan(39°):
3.05 = 1.99 + 14.5 * tan(39°) – 4.9 * (14.5² / (v₀² cos²(39°)))
Now, we plug in the values for the trigonometric functions and rearrange to solve for v₀:
3.05 = 1.99 + 14.5 * (0.8098) – 4.9 * (210.25 / (v₀² * (0.7771)²))
3.05 = 1.99 + 11.742 – (1030.225 / (v₀² * 0.6039))
3.05 = 13.732 – (1705.9 / v₀²)
1705.9 / v₀² = 13.732 – 3.05
1705.9 / v₀² = 10.682
v₀² = 1705.9 / 10.682
v₀² ≈ 159.7
v₀ ≈ √159.7
v₀ ≈ 12.64 m/s
