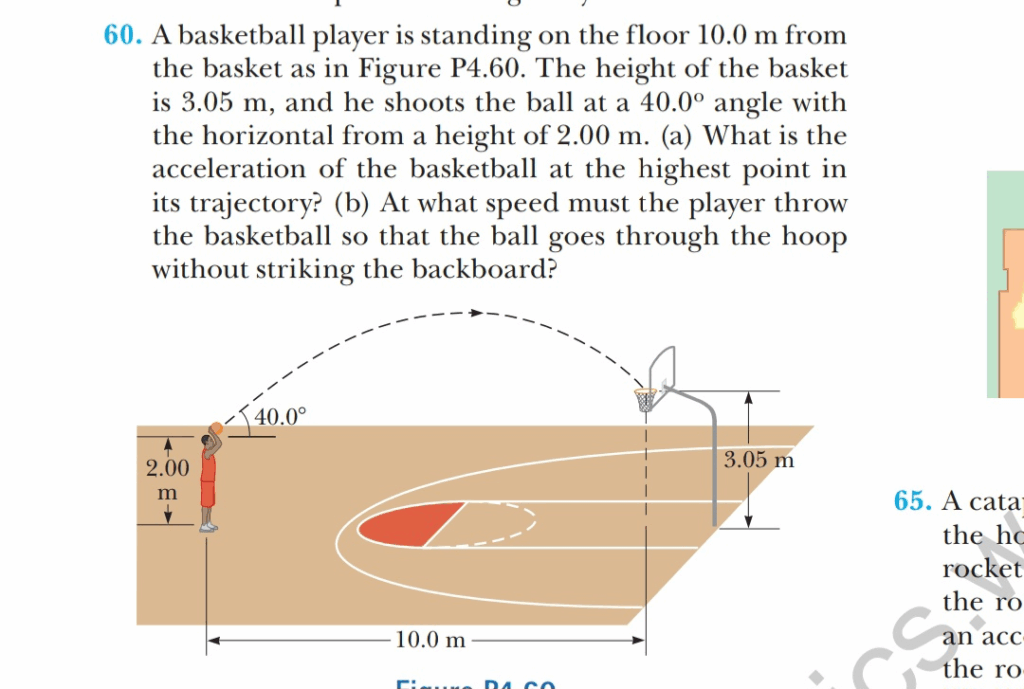
A basketball player is standing on the floor 10.0 m from the basket as in Figure P4.60.

A basketball player is standing on the floor 10.0 m from the basket as in Figure P4.60.

The Correct Answer and Explanation is:

Here are the answers to the physics problem.

(a) 9.80 m/s² downwards
(b) 10.7 m/s

Explanation

(a) Acceleration at the Highest Point

Once the basketball leaves the player’s hands, the only significant force acting on it is gravity (assuming air resistance is negligible). According to Newton’s second law, this constant downward force produces a constant downward acceleration. This acceleration is the acceleration due to gravity, g, which is approximately 9.80 m/s².

This acceleration remains constant throughout the entire flight of the ball. Even at the highest point of its trajectory, where the vertical component of its velocity is momentarily zero, the force of gravity is still acting on it. Therefore, the acceleration of the basketball at the highest point is 9.80 m/s² directed downwards.

(b) Initial Speed of the Throw

To find the initial speed (v₀) required for the ball to reach the hoop, we analyze its motion in two dimensions: horizontal and vertical.

Set up the coordinate system: Let the initial position of the ball be (x₀, y₀) = (0, 2.00 m). The final position, the hoop, is at (x, y) = (10.0 m, 3.05 m). The launch angle θ is 40.0°.
Analyze the motion:
- Horizontal Motion: The horizontal velocity (vₓ) is constant.
  x = v₀ₓ * t
  v₀ₓ = v₀ * cos(40.0°)
  So, 10.0 = (v₀ * cos(40.0°)) * t
  We can express the time of flight (t) as: t = 10.0 / (v₀ * cos(40.0°))
- Vertical Motion: The vertical motion has a constant downward acceleration of g = 9.80 m/s².
  y = y₀ + v₀y * t – (1/2)gt²
  v₀y = v₀ * sin(40.0°)
  Substituting the known values:
  3.05 = 2.00 + (v₀ * sin(40.0°)) * t – (1/2)(9.80)t²
Solve for the initial speed (v₀):
Now, substitute the expression for t from the horizontal motion into the vertical motion equation. This eliminates t and allows us to solve for v₀.1.05 = (v₀ * sin(40.0°)) * [10.0 / (v₀ * cos(40.0°))] – 4.90 * [10.0 / (v₀ * cos(40.0°))]²
1.05 = 10.0 * tan(40.0°) – 490 / (v₀² * cos²(40.0°))Now, solve for v₀:
1.05 = 10.0 * (0.8391) – 490 / (v₀² * (0.7660)²)
1.05 = 8.391 – 490 / (v₀² * 0.5868)
1.05 = 8.391 – 835.0 / v₀²
835.0 / v₀² = 8.391 – 1.05 = 7.341
v₀² = 835.0 / 7.341 = 113.75
v₀ = √113.75 ≈ 10.665 m/sRounding to three significant figures, the required initial speed is 10.7 m/s.

Explanation

Related Posts