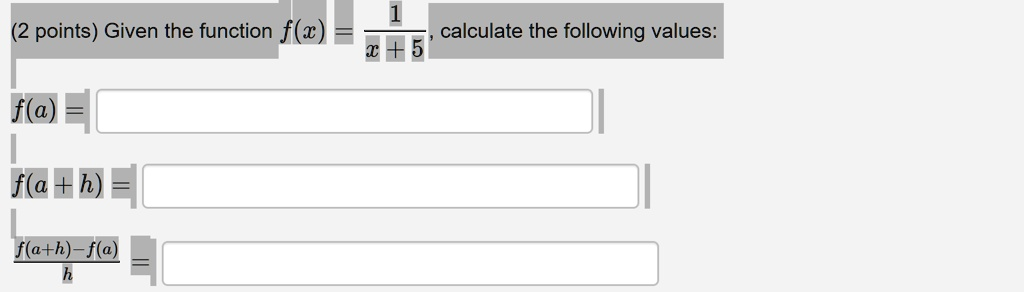
points) Given the function f(x)=1x+5, calculate the following values:
The Correct Answer and Explanation is:
Of course. Here are the correct answers and a detailed explanation for the problem.
Answers:
- f(a) = 1 / (a + 5)
- f(a + h) = 1 / (a + h + 5)
- (f(a + h) – f(a)) / h = -1 / ((a + 5)(a + h + 5))
Explanation:
This problem asks you to work with function notation and then to calculate and simplify the difference quotient, which is a fundamental concept in calculus used to define the derivative of a function.
1. Calculating f(a)
The first step is to evaluate the function f(x) at the value x = a. The original function is given as f(x) = 1 / (x + 5). To find f(a), we simply replace every instance of x in the function’s formula with a.
- Original function: f(x) = 1 / (x + 5)
- Substitute x with a: f(a) = 1 / (a + 5)
This expression cannot be simplified further, so it is the final answer for the first part.
2. Calculating f(a + h)
The second step is similar, but this time we evaluate the function at x = a + h. We substitute the entire expression (a + h) for x in the original function.
- Original function: f(x) = 1 / (x + 5)
- Substitute x with (a + h): f(a + h) = 1 / ((a + h) + 5)
- Removing the inner parentheses gives: f(a + h) = 1 / (a + h + 5)
This is the final simplified expression for the second part.
3. Calculating the Difference Quotient: (f(a + h) – f(a)) / h
This final part requires you to use the results from the first two steps and perform algebraic simplification. We start by substituting the expressions for f(a + h) and f(a) into the difference quotient formula.
- Start with the formula: (f(a + h) – f(a)) / h
- Substitute the expressions: [ (1 / (a + h + 5)) – (1 / (a + 5)) ] / h
This is a complex fraction. The first step to simplifying it is to combine the two fractions in the numerator. To do this, we find a common denominator, which is the product of the two individual denominators: (a + h + 5)(a + 5).
- Rewrite the numerator with the common denominator:
[ (1 * (a + 5)) / ((a + h + 5)(a + 5)) ] – [ (1 * (a + h + 5)) / ((a + h + 5)(a + 5)) ] - Combine the fractions over the single denominator:
( (a + 5) – (a + h + 5) ) / ( (a + h + 5)(a + 5) ) - Simplify the new numerator by distributing the negative sign and combining like terms:
( a + 5 – a – h – 5 ) / ( (a + h + 5)(a + 5) )
The a and -a cancel out, and the 5 and -5 cancel out, leaving just -h. - The simplified numerator is: -h / ( (a + h + 5)(a + 5) )
Now, we place this back into the full difference quotient expression:
- ( -h / ((a + h + 5)(a + 5)) ) / h
Dividing by h is the same as multiplying by its reciprocal, 1/h.
- ( -h / ((a + h + 5)(a + 5)) ) * (1 / h)
Finally, we can cancel the h in the numerator with the h in the denominator, which leaves -1 in the numerator.
- The final simplified answer is: -1 / ( (a + h + 5)(a + 5) )
