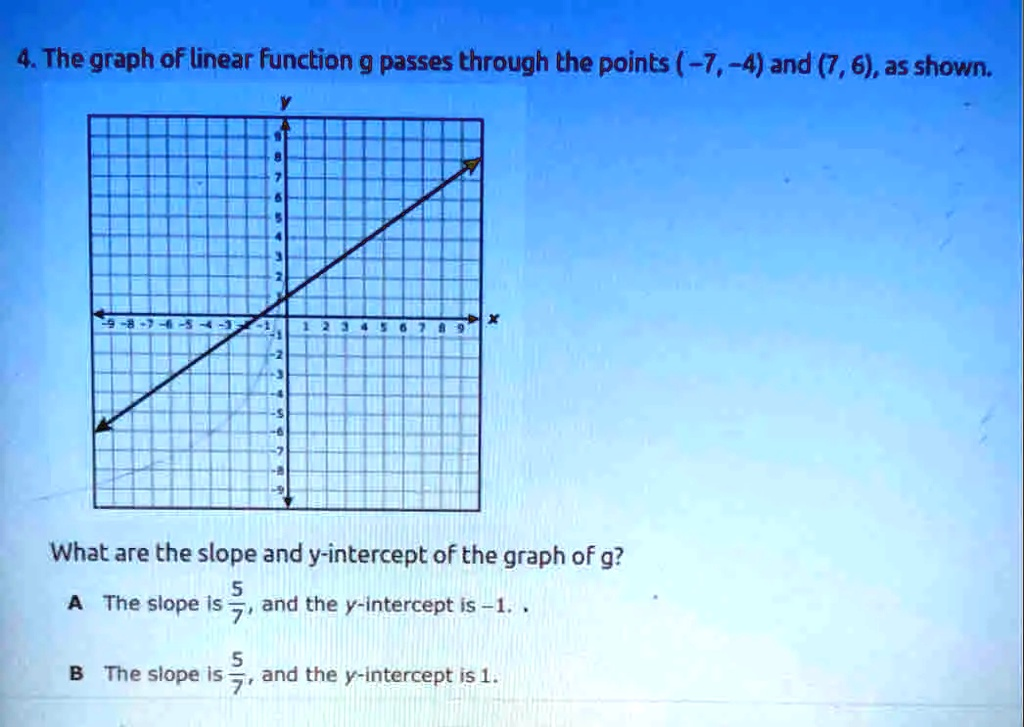
The graph of linear function g passes through the points (-7, -4) and (7, 6), as shown. What are the slope and y-intercept of the graph of g? A The slope is
, and the y-intercept is -1. B The slope is
, and the y-intercept is 1.
The Correct Answer and Explanation is:
The correct answer is B The slope is 5/7, and the y-intercept is 1.
Here is a detailed explanation of how to determine the slope and y-intercept for the linear function g.
Finding the Slope
The slope of a line measures its steepness and is often described as “rise over run”. We can find the slope in two ways: by using the coordinates of the two given points or by observing the rise and run directly from the graph.
- Using the Slope Formula: The formula for the slope (m) of a line that passes through two points (x₁, y₁) and (x₂, y₂) is m = (y₂ – y₁) / (x₂ – x₁). The problem provides the points (-7, -4) and (7, 6). Let’s substitute these values into the formula:
- m = (6 – (-4)) / (7 – (-7))
- m = (6 + 4) / (7 + 7)
- m = 10 / 14
- Simplifying this fraction by dividing both the numerator and the denominator by their greatest common divisor, which is 2, gives us m = 5/7.
- Using the Graph (Rise over Run): To find the slope from the graph, we can count the vertical change (rise) and the horizontal change (run) between the two points.
- Rise: Starting from the point (-7, -4), we move vertically upwards to be on the same horizontal level as the second point (7, 6). The change in the y-value is from -4 to 6, which is a total rise of 10 units.
- Run: From that new position, we move horizontally to the right to reach the point (7, 6). The change in the x-value is from -7 to 7, which is a total run of 14 units.
- The slope is the rise divided by the run, so m = 10/14, which simplifies to 5/7.
Finding the y-intercept
The y-intercept is the point where the line crosses the vertical y-axis. At this point, the x-coordinate is always zero.
- Reading from the Graph: By looking at the provided graph, we can visually identify where the line intersects the y-axis. The line passes through the y-axis at the value y = 1. Therefore, the y-intercept is 1.
- Using the Slope-Intercept Equation: The equation of a line is y = mx + b, where m is the slope and b is the y-intercept. We have already calculated the slope as 5/7. We can now use one of the given points, such as (7, 6), and substitute the values of x, y, and m into the equation to solve for b.
- y = mx + b
- 6 = (5/7)(7) + b
- 6 = 5 + b
- Subtracting 5 from both sides gives us b = 1.
Both methods confirm that the slope is 5/7 and the y-intercept is 1, which corresponds to option B.
