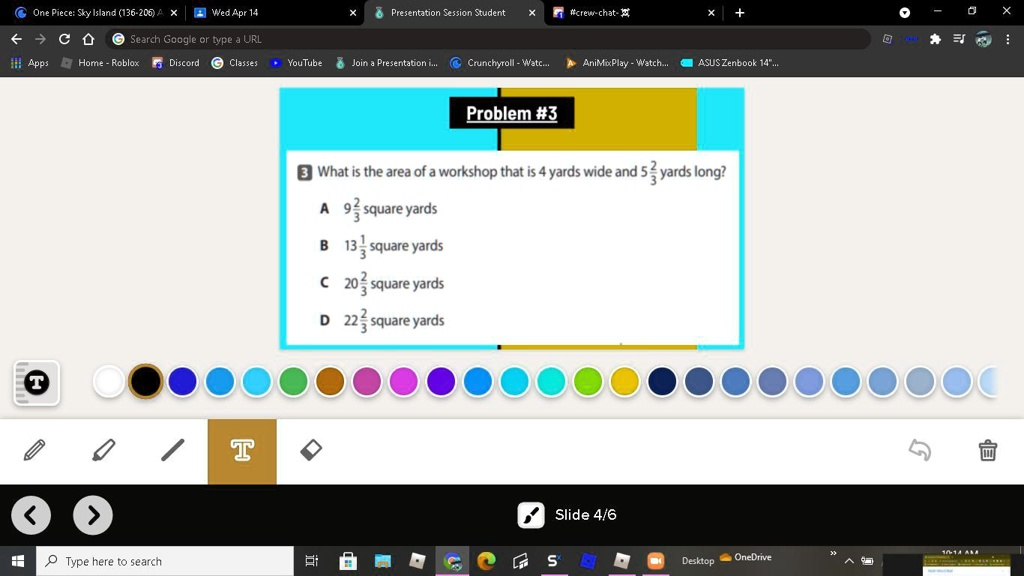
What is the area of a workshop that is 4 yards wide and 5 2/3 yards long
The Correct Answer and Explanation is:
The correct answer is D) 22 2/3 square yards.
To solve this problem, you need to find the area of the workshop. Since the workshop has a specified width and length, we can assume it is a rectangular space. The formula to calculate the area of a rectangle is by multiplying its length by its width (Area = length × width).
The problem provides the following dimensions:
- Width = 4 yards
- Length = 5 2/3 yards
To begin the calculation, we multiply these two values:
Area = 4 × 5 2/3
Multiplying a whole number by a mixed number is most easily done by first converting the mixed number into an improper fraction. To convert 5 2/3 into an improper fraction, you multiply the whole number (5) by the fraction’s denominator (3), and then add the numerator (2). The result becomes the new numerator, while the denominator remains the same.
So, (5 × 3) + 2 = 15 + 2 = 17. The improper fraction is 17/3.
Now, the multiplication problem is:
Area = 4 × 17/3
To multiply a whole number by a fraction, you can express the whole number as a fraction over 1 (4 becomes 4/1). Then, multiply the numerators together and the denominators together.
Area = (4/1) × (17/3) = (4 × 17) / (1 × 3) = 68/3
The result is an improper fraction, 68/3. To make it comparable with the answer choices, we must convert it back into a mixed number. We do this by dividing the numerator (68) by the denominator (3).
68 ÷ 3 = 22 with a remainder of 2.
The quotient (22) is the whole number part of the mixed number. The remainder (2) is the new numerator, and the denominator (3) stays the same. Therefore, the area is 22 2/3 square yards. This result matches option D
