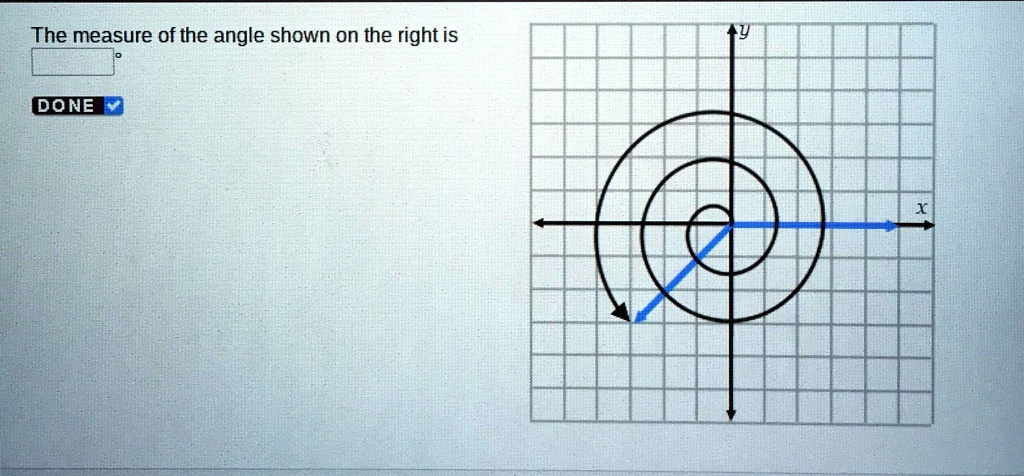
The measure of the angle shown on the right is
The Correct Answer and Explanation is:
The measure of the angle shown on the right is -495°
Explanation:
To determine the measure of the angle shown in the coordinate plane, we need to analyze its initial side, terminal side, and the direction and magnitude of its rotation.
- Initial Side and Direction of Rotation: In standard position, an angle’s initial side always lies on the positive x-axis. The curved arrow in the diagram indicates the rotation from this initial side. Since the arrow moves in a clockwise direction, the measure of the angle will be negative.
- Magnitude of Rotation: The arrow makes more than one full circle. We can see it completes one full revolution and then continues to its final position. A full clockwise revolution is equal to -360°.
- Terminal Side and Reference Angle: The terminal side of the angle is the blue ray that ends in the third quadrant. By examining the grid, we can see that this ray passes through the point (-2, -2). To find the angle of this terminal side, we can first find its reference angle. The reference angle is the acute angle that the terminal side makes with the x-axis. For a point (x, y) like (-2, -2), we can form a right triangle with the x-axis. The lengths of the sides adjacent and opposite to the origin are both 2 units. The tangent of the reference angle (α) is given by:tan(α) = |opposite/adjacent| = |-2/-2| = 1
α = tan⁻¹(1) = 45° - Angle of the Terminal Portion: Since the terminal side is in the third quadrant, the additional rotation past the full circle is more than 90° but less than 180° in the clockwise direction. The angle measured clockwise from the positive x-axis to the terminal side is -90° (to the negative y-axis) plus another -45° (to the terminal ray), which gives -135°. Alternatively, the positive angle to the terminal side is 180° + 45° = 225°. The negative coterminal angle is 225° – 360° = -135°.
- Total Angle Calculation: The total angle is the sum of the full clockwise rotation and the additional clockwise rotation to the terminal side.Total Angle = (Full Clockwise Rotation) + (Additional Clockwise Rotation)
Total Angle = -360° + (-135°)
Total Angle = -495°
Therefore, the measure of the angle shown is -495°.
