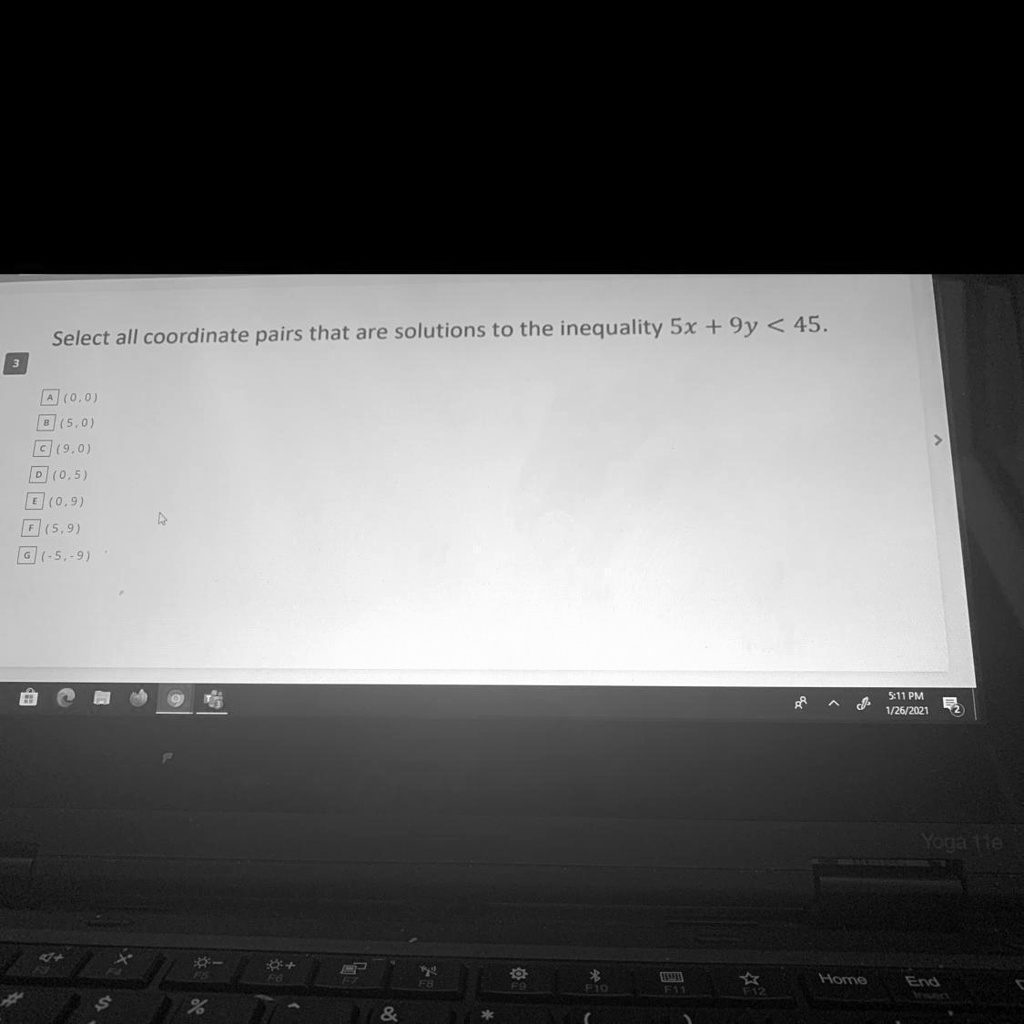
The Correct Answer and Explanation is:
The inequality given is 5x+9y<455x + 9y < 455x+9y<45, and we are asked to determine which coordinate pairs satisfy this inequality.
Let’s test each of the coordinate pairs provided in the options:
- A: (0, 0)
Substitute x=0x = 0x=0 and y=0y = 0y=0 into the inequality: 5(0)+9(0)=0<455(0) + 9(0) = 0 < 455(0)+9(0)=0<45 This is true. Therefore, (0,0)(0, 0)(0,0) is a solution. - B: (5, 0)
Substitute x=5x = 5x=5 and y=0y = 0y=0 into the inequality: 5(5)+9(0)=25<455(5) + 9(0) = 25 < 455(5)+9(0)=25<45 This is true. Therefore, (5,0)(5, 0)(5,0) is a solution. - C: (9, 0)
Substitute x=9x = 9x=9 and y=0y = 0y=0 into the inequality: 5(9)+9(0)=45≮455(9) + 9(0) = 45 \not< 455(9)+9(0)=45<45 This is false. Therefore, (9,0)(9, 0)(9,0) is not a solution. - D: (0, 5)
Substitute x=0x = 0x=0 and y=5y = 5y=5 into the inequality: 5(0)+9(5)=45≮455(0) + 9(5) = 45 \not< 455(0)+9(5)=45<45 This is false. Therefore, (0,5)(0, 5)(0,5) is not a solution. - E: (0, 9)
Substitute x=0x = 0x=0 and y=9y = 9y=9 into the inequality: 5(0)+9(9)=81≮455(0) + 9(9) = 81 \not< 455(0)+9(9)=81<45 This is false. Therefore, (0,9)(0, 9)(0,9) is not a solution. - F: (5, 9)
Substitute x=5x = 5x=5 and y=9y = 9y=9 into the inequality: 5(5)+9(9)=25+81=106≮455(5) + 9(9) = 25 + 81 = 106 \not< 455(5)+9(9)=25+81=106<45 This is false. Therefore, (5,9)(5, 9)(5,9) is not a solution. - G: (-5, -9)
Substitute x=−5x = -5x=−5 and y=−9y = -9y=−9 into the inequality: 5(−5)+9(−9)=−25−81=−106<455(-5) + 9(-9) = -25 – 81 = -106 < 455(−5)+9(−9)=−25−81=−106<45 This is true. Therefore, (−5,−9)(-5, -9)(−5,−9) is a solution.
Conclusion:
The coordinate pairs that satisfy the inequality 5x+9y<455x + 9y < 455x+9y<45 are:
- A: (0, 0)
- B: (5, 0)
- G: (-5, -9)
