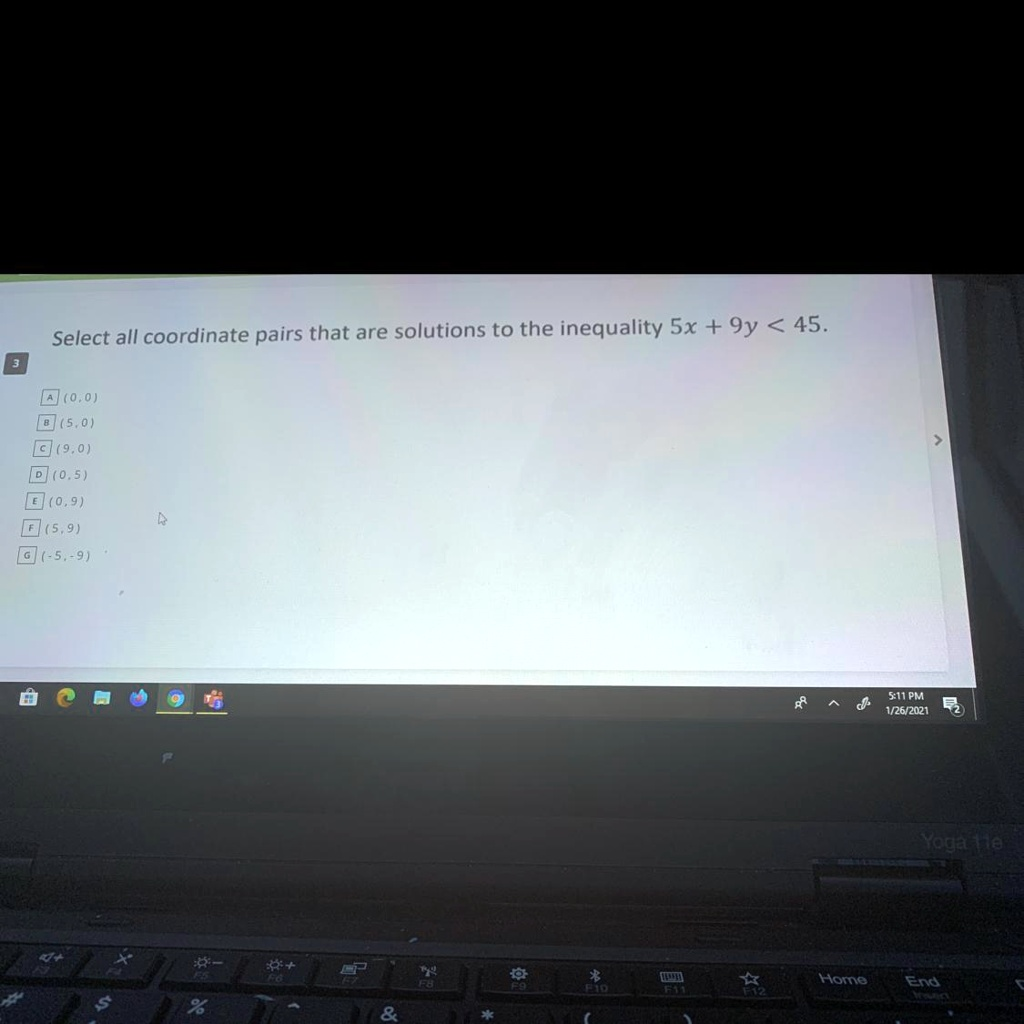
The Correct Answer and Explanation is:
The correct coordinate pairs that are solutions to the inequality are:
A (0, 0)
B (5, 0)
G (-5, -9)
To determine which coordinate pairs are solutions to the inequality 5x + 9y < 45, we must substitute the x and y values from each given pair into the inequality. If the resulting mathematical statement is true, the coordinate pair is a solution. The problem requires us to find all pairs that satisfy this condition.
Let’s test each option systematically:
- A (0, 0): We substitute x = 0 and y = 0.
5(0) + 9(0) < 45
0 + 0 < 45
0 < 45. This statement is true, so (0, 0) is a solution. - B (5, 0): We substitute x = 5 and y = 0.
5(5) + 9(0) < 45
25 + 0 < 45
25 < 45. This statement is true, so (5, 0) is a solution. - C (9, 0): We substitute x = 9 and y = 0.
5(9) + 9(0) < 45
45 + 0 < 45
45 < 45. This statement is false. 45 is equal to 45, not strictly less than it. Thus, (9, 0) is not a solution. - D (0, 5): We substitute x = 0 and y = 5.
5(0) + 9(5) < 45
0 + 45 < 45
45 < 45. This statement is also false for the same reason as option C. Thus, (0, 5) is not a solution. - E (0, 9): We substitute x = 0 and y = 9.
5(0) + 9(9) < 45
0 + 81 < 45
81 < 45. This statement is false. - F (5, 9): We substitute x = 5 and y = 9.
5(5) + 9(9) < 45
25 + 81 < 45
106 < 45. This statement is false. - G (-5, -9): We substitute x = -5 and y = -9.
5(-5) + 9(-9) < 45
-25 – 81 < 45
-106 < 45. This statement is true. A negative number is always less than a positive number. Therefore, (-5, -9) is a solution.
After checking all the options, we find that the coordinate pairs (0, 0), (5, 0), and (-5, -9) are the only ones that make the inequality true
