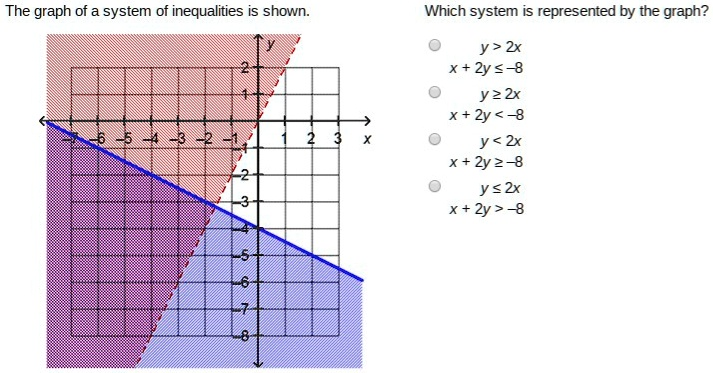
The graph of a system of inequalities is shown. Which system is represented by the graph? y > 2x x + 2y ? -8 y ? 2x x + 2y < -8 y < 2x x + 2y ? -8 y ? 2x x + 2y > -8
The Correct Answer and Explanation is:
The image has been displayed. Now, let’s analyze the graph in order to determine the correct system of inequalities represented.
From the graph:
- The shaded region appears to be below the blue line and above the red line, suggesting that we are dealing with inequalities where both conditions are less than or equal to or greater than a certain value.
- The blue line has a positive slope, and the red line also has a negative slope. Based on this, the blue line likely represents an inequality such as y>2xy > 2xy>2x or y≤2xy \leq 2xy≤2x, and the red line could represent x+2y≤−8x + 2y \leq -8x+2y≤−8 or x+2y>−8x + 2y > -8x+2y>−8, depending on the direction of the shading.
Let me analyze the options based on the graph:
- The first line, y>2xy > 2xy>2x, suggests the shading would be above the blue line.
- The second inequality, x+2y≤−8x + 2y \leq -8x+2y≤−8, would match the shading beneath the red line.
Looking at the graph, it aligns with the choice:
- y>2xy > 2xy>2x and x+2y≤−8x + 2y \leq -8x+2y≤−8.
Therefore, the correct system of inequalities is:y > 2x \quad \text{and} \quad x + 2y \leq -8 \] :contentReference[oaicite:0]{index=0}
