The Correct Answer and Explanation is:
The correct choice is:
A. The solution is (0, -5).
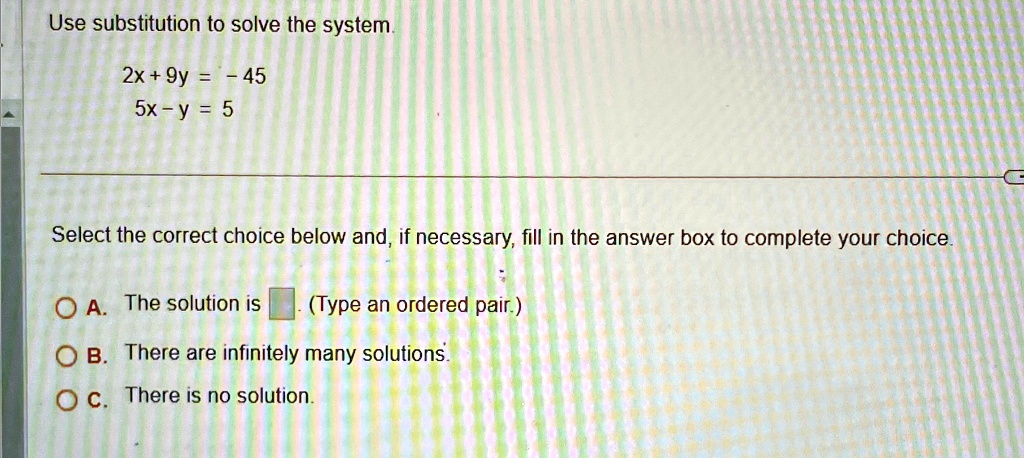
To solve the system of equations using the substitution method, we first need to isolate one variable in one of the equations. The given system is:
- 2x + 9y = -45
- 5x – y = 5
The second equation, 5x – y = 5, is the easiest to rearrange to solve for one variable. We can isolate y by first subtracting 5x from both sides, which gives us -y = 5 – 5x. Then, by multiplying the entire equation by -1, we get y = -5 + 5x, or more simply, y = 5x – 5.
Now that we have an expression for y, we substitute it into the first equation, 2x + 9y = -45. This step replaces the y variable in the first equation with our new expression involving x. The substitution results in the following equation with only one variable, x:
2x + 9(5x – 5) = -45
Next, we solve this equation for x. We start by distributing the 9 into the parentheses:
2x + 45x – 45 = -45
Combine the x terms on the left side:
47x – 45 = -45
To isolate the term with x, we add 45 to both sides of the equation:
47x = 0
Finally, we divide both sides by 47 to find the value of x:
x = 0
With the value of x found, we can now find the value of y. We substitute x = 0 back into the equation we derived earlier, y = 5x – 5:
y = 5(0) – 5
y = 0 – 5
y = -5
The solution to the system is the ordered pair (x, y), which is (0, -5). We can verify this solution by plugging these values back into both original equations to ensure they hold true.
