The Correct Answer and Explanation is:1
Correct Answer: The pKₐ of nitrous acid is 3.35.
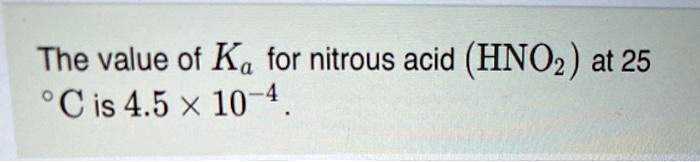
Based on the information provided, the acid dissociation constant, or Kₐ, for nitrous acid (HNO₂) at 25 °C is 4.5 × 10⁻⁴. This value is a quantitative measure of the strength of an acid in solution.
The Kₐ value arises from the equilibrium expression for the dissociation of a weak acid in water. For nitrous acid, the reaction is:
HNO₂(aq) + H₂O(l) ⇌ H₃O⁺(aq) + NO₂⁻(aq)
The small magnitude of the Kₐ value (4.5 × 10⁻⁴) confirms that nitrous acid is a weak acid. This means that when it is dissolved in water, only a small fraction of the HNO₂ molecules donate a proton to form hydronium ions (H₃O⁺) and nitrite ions (NO₂⁻). The equilibrium strongly favors the undissociated acid on the left side of the equation.
A common and convenient way to express acid strength is by using the pKₐ, which is the negative base-10 logarithm of the Kₐ value. The calculation is as follows:
pKₐ = -log(Kₐ)
pKₐ = -log(4.5 × 10⁻⁴)
pKₐ ≈ 3.35
A lower pKₐ value corresponds to a stronger acid. This logarithmic scale makes it easier to compare the relative strengths of different acids.
Furthermore, we can use the Kₐ of nitrous acid to find the base dissociation constant (Kₑ) for its conjugate base, the nitrite ion (NO₂⁻). The relationship between Kₐ, Kₑ, and the ion product constant for water (Kₐ, which is 1.0 × 10⁻¹⁴ at 25 °C) is Kₐ × Kₑ = Kₐ.
Kₑ for NO₂⁻ = Kₐ / Kₐ = (1.0 × 10⁻¹⁴) / (4.5 × 10⁻⁴) ≈ 2.2 × 10⁻¹¹. This small Kₑ value indicates that nitrite is a weak base, which is expected for the conjugate base of a weak acid.
