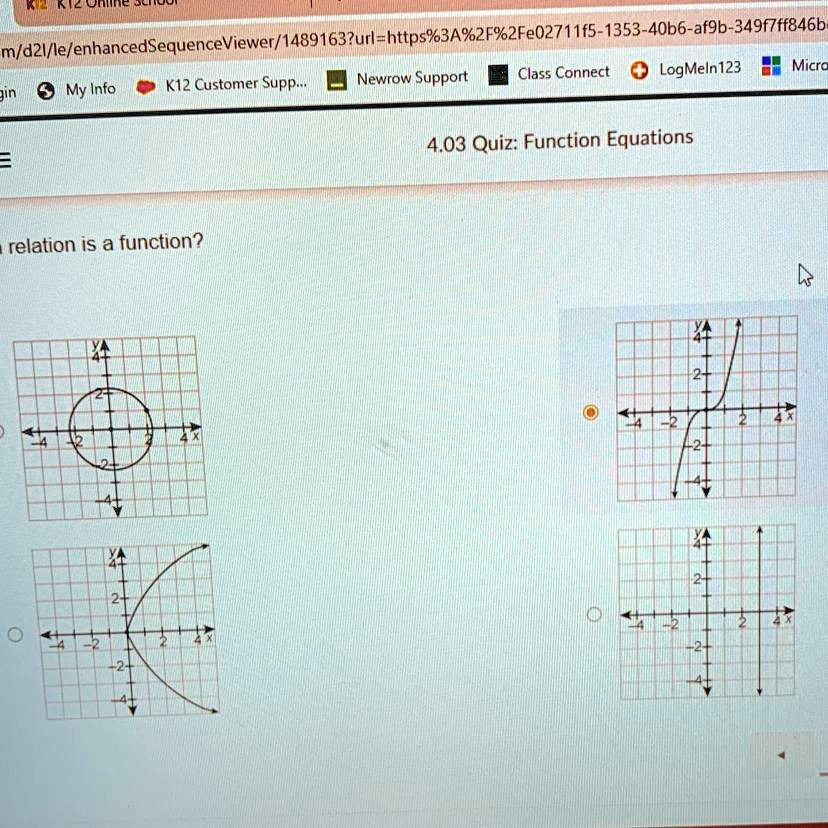
Relation is a function
The Correct Answer and Explanation is:
The correct answer is the graph located in the top right corner.
To determine which of the graphed relations is a function, we must use the definition of a function. A relation is considered a function if and only if every input value (x-value) corresponds to exactly one unique output value (y-value). A simple and reliable way to check this on a graph is by using the Vertical Line Test.
The Vertical Line Test states that if you can draw a vertical line anywhere on the graph that intersects the curve at more than one point, the relation is not a function. This is because a single vertical line represents a constant x-value, and multiple intersection points would mean that one x-value has multiple y-values, violating the core rule of functions.
Let’s apply this test to each of the four graphs:
- Top Left Graph (Circle): If you draw a vertical line through any part of the circle’s interior, for example at x = 1, the line will intersect the circle at two distinct points. Since one x-value corresponds to two y-values, this relation is not a function.
- Bottom Left Graph (Sideways Parabola): Similar to the circle, a vertical line drawn to the right of the y-axis, such as at x = 2, will cross the parabola in two places. This means it fails the Vertical Line Test and is not a function.
- Bottom Right Graph (Vertical Line): This graph represents a single x-value that is paired with an infinite number of y-values. A vertical line drawn directly on top of this graph would touch it at every point. This is a clear violation of the function definition.
- Top Right Graph (S-shaped Curve): If you scan a vertical line across this entire graph from left to right, you will find that the line only ever intersects the curve at a single point. For every x-value, there is only one corresponding y-value. This graph successfully passes the Vertical Line Test.
Therefore, the only relation that represents a function is the one depicted in the top right corner.
