y 5 4 3 2 1 -5 -4 -3 -2 -1 1 2 3 4 5 x -2 -3 -4 -5 Which
The Correct Answer and Explanation is:
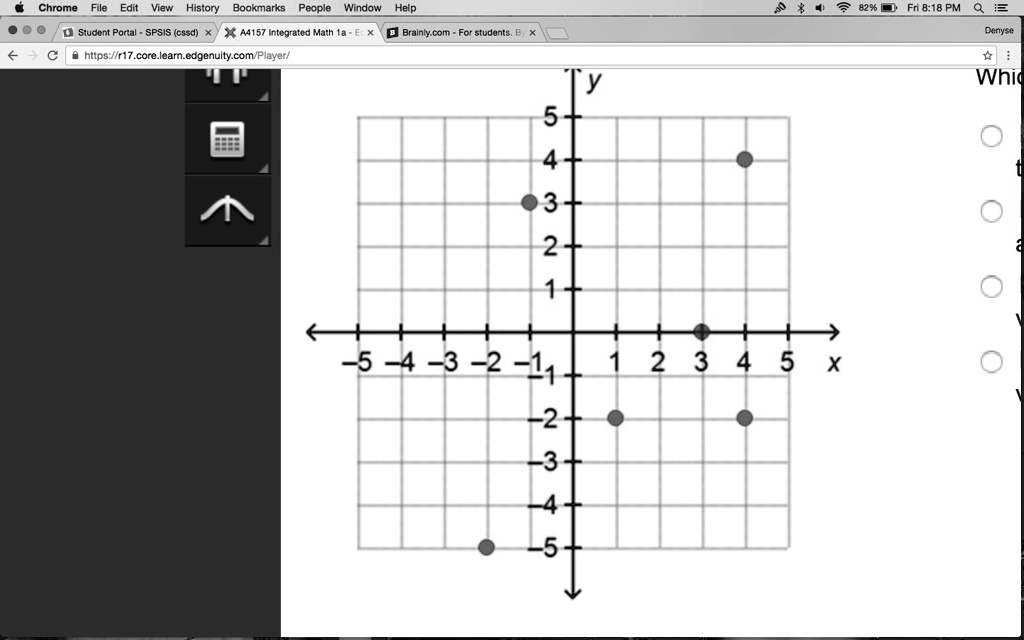
Based on the graph provided, the correct answer is that the relation shown is not a function.
A fundamental concept in mathematics is the definition of a function. A relation, which is any set of ordered pairs (x, y), qualifies as a function only if each unique input value, or x-coordinate, corresponds to exactly one output value, or y-coordinate. If any single input is paired with more than one output, the relation fails to be a function.
To determine if the plotted points in the image represent a function, we must examine the coordinates of each point. The points on the graph are located at the coordinates (-2, -5), (-1, 3), (1, -2), (4, 4), and (4, -2). When we analyze these ordered pairs, we must look for any repeated x-values that are paired with different y-values.
A careful inspection reveals a clear violation of the function rule. The x-value of 4 appears in two different ordered pairs: (4, 4) and (4, -2). This means the single input of 4 is mapped to two distinct outputs, 4 and -2. Because an input has more than one corresponding output, the relation is definitively not a function.
This conclusion can also be reached visually using what is known as the vertical line test. This test is a simple graphical method for identifying functions. If it is possible to draw any vertical line that intersects a graph at more than one point, the graph does not represent a function. In this specific case, a vertical line drawn on the coordinate plane at the position x = 4 would pass through both the point (4, 4) and the point (4, -2). Since this single vertical line intersects the set of plotted points twice, it provides visual confirmation that the relation is not a function. Therefore, the collection of points fails the primary requirement of a function.
