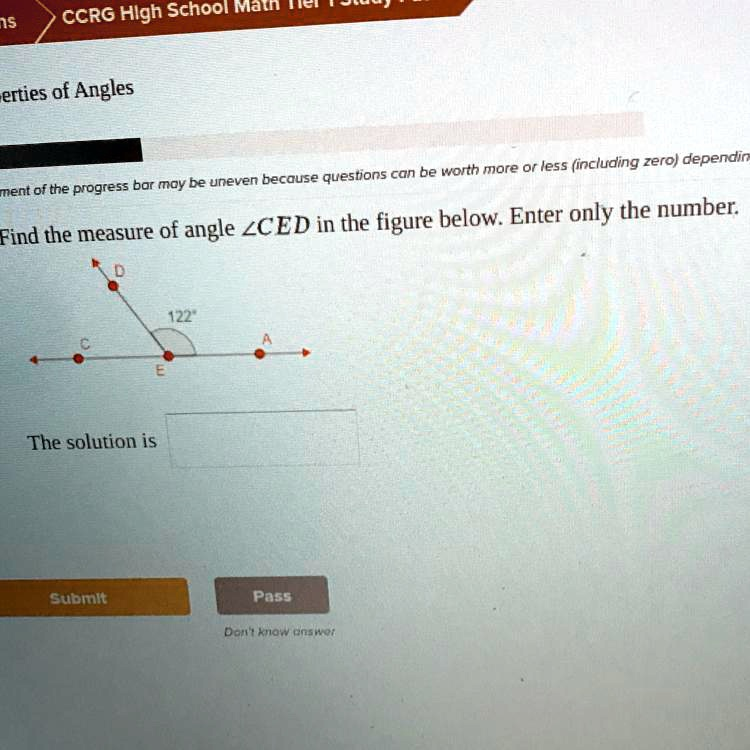
Find the measure of angle in the figure below.
The Correct Answer and Explanation is:
The correct answer is 58.
To find the measure of angle ∠CED, we need to understand the properties of angles on a straight line. The image displays a straight line passing through points C, E, and A. A straight line represents a straight angle, which by definition measures 180 degrees. Therefore, the total measure of the angle formed by the line, ∠CEA, is 180 degrees.
In the figure, a ray ED originates from point E on the line. This ray divides the straight angle ∠CEA into two adjacent angles: ∠CED and ∠DEA. When two angles are adjacent and their non-common sides form a straight line, they are called supplementary angles. A key property of supplementary angles is that their measures add up to 180 degrees.
This gives us the equation:
m∠CED + m∠DEA = 180°
From the diagram, we are given the measure of one of the angles:
m∠DEA = 122°
Now we can substitute this known value into our equation to solve for the measure of angle ∠CED:
m∠CED + 122° = 180°
To find the value of m∠CED, we isolate it by subtracting 122° from both sides of the equation:
m∠CED = 180° – 122°
Performing the subtraction gives us the result:
m∠CED = 58°
Therefore, the measure of angle ∠CED is 58 degrees. The question asks to enter only the number, so the solution is 58.
