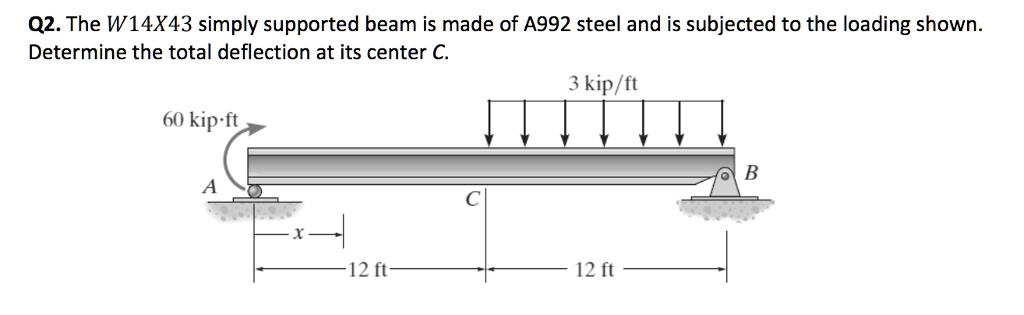
The W14X43 simply supported beam is made of A992 steel and is subjected to the loading shown. Determine the total deflection at its center C. 60 kip\text{-}ft 3 kip/ft A 12 ft C 12 ft B
The Correct Answer and Explanation is:
Here is the step-by-step solution to determine the total deflection at the center C of the beam.
Final Answer:
The total deflection at the center C of the beam is 0.601 inches downward.
Explanation:
To find the total deflection at point C, we will use the principle of superposition. This principle allows us to calculate the deflection caused by each load separately and then add them together algebraically. The total deflection at C (δ_C) is the sum of the deflection due to the concentrated moment at A (δ_C,M) and the deflection due to the uniformly distributed load (δ_C,w).
1. Material and Section Properties:
First, we need the properties of the A992 steel and the W14x43 beam section.
- Modulus of Elasticity (E) for A992 Steel: E = 29,000 ksi (kips per square inch).
- Moment of Inertia (I) for a W14x43 section: From a standard steel properties table, I = 428 in⁴.
For consistency, we will convert all units to kips and inches.
- Beam Length (L): L = 24 ft = 24 ft × 12 in/ft = 288 in.
- Concentrated Moment (M₀): M₀ = 60 kip-ft = 60 kip-ft × 12 in/ft = 720 kip-in.
- Distributed Load (w): w = 3 kip/ft = 3 kip/ft / (12 in/ft) = 0.25 kip/in.
2. Deflection due to the Concentrated Moment (δ_C,M):
The first case is a simply supported beam with a concentrated moment M₀ at support A. The standard formula for deflection at the center (x = L/2) is:
δ_C,M = (M₀ * L²) / (16 * E * I)
The counter-clockwise moment at the left support will cause the center of the beam to deflect upwards. We will consider upward deflection as negative.
δ_C,M = – (720 kip-in * (288 in)²) / (16 * 29,000 ksi * 428 in⁴)
δ_C,M = – 59,719,680 / 198,592,000 kip-in
δ_C,M = -0.301 in (upward)
3. Deflection due to the Distributed Load (δ_C,w):
The second case is a simply supported beam with a uniform load w applied from the center C (x = L/2) to the right support B (x = L). The standard formula for deflection at the center (x = L/2) for this loading case is:
δ_C,w = (5 * w * L⁴) / (768 * E * I)
This load acts downwards, so the deflection will be downwards (positive).
δ_C,w = (5 * 0.25 kip/in * (288 in)⁴) / (768 * 29,000 ksi * 428 in⁴)
δ_C,w = (1.25 * 6,879,707,136) / 9,532,416,000 kip-in
δ_C,w = 8,599,633,920 / 9,532,416,000 kip-in
δ_C,w = +0.902 in (downward)
4. Total Deflection at Center C:
Finally, we add the two deflections together:
δ_C = δ_C,M + δ_C,w
δ_C = -0.301 in + 0.902 in
δ_C = +0.601 in
The positive sign indicates that the net deflection is in the downward direction.
