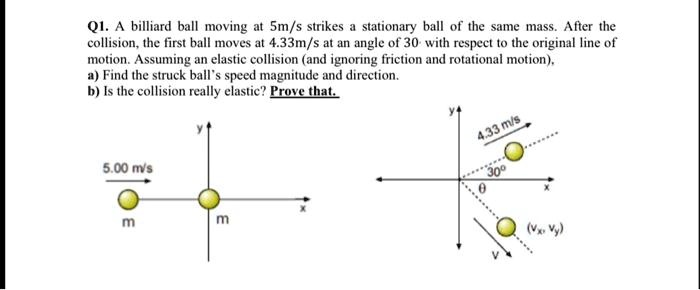
A billiard ball moving at 5m/s strikes a stationary ball of the same mass. After the collision, the first ball moves at 4.33m/s at an angle of 30 with respect to the original line of motion. Assuming an elastic collision (and ignoring friction and rotational motion), a) Find the struck ball’s speed magnitude and direction. b) Is the collision really elastic? Prove that.
The Correct Answer and Explanation is:
Here is the solution to the physics problem.
This problem involves a two-dimensional collision between two billiard balls of equal mass. We can solve this by applying the principle of conservation of linear momentum. Since momentum is a vector quantity, we must conserve it independently in both the horizontal (x) and vertical (y) directions.
a) Find the struck ball’s speed magnitude and direction.
To find the final velocity of the second ball, we will set up conservation of momentum equations. Let ‘m’ be the mass of each ball. Let the initial velocity of the first ball be v1i and the second ball be v2i. Let their final velocities be v1f and v2f, respectively. The problem provides that v1i = 5.00 m/s along the x-axis, v2i = 0, and v1f has a magnitude of 4.33 m/s at an angle of 30 degrees.
Conservation of Momentum in the x-direction:
The total initial momentum in the x-direction must equal the total final momentum in the x-direction.
Initial x-momentum = m * v1ix + m * v2ix = m * (5.00) + m * (0) = 5.00m
Final x-momentum = m * v1fx + m * v2fx = m * (4.33 * cos(30°)) + m * v2fx
Setting them equal and canceling ‘m’:
5.00 = 4.33 * cos(30°) + v2fx
5.00 = 4.33 * (0.866) + v2fx
5.00 = 3.75 + v2fx
v2fx = 5.00 – 3.75 = 1.25 m/s
Conservation of Momentum in the y-direction:
The total initial momentum in the y-direction was zero, so the total final momentum in the y-direction must also be zero.
Initial y-momentum = m * v1iy + m * v2iy = m * (0) + m * (0) = 0
Final y-momentum = m * v1fy + m * v2fy = m * (4.33 * sin(30°)) + m * v2fy
Setting them equal and canceling ‘m’:
0 = 4.33 * sin(30°) + v2fy
0 = 4.33 * (0.5) + v2fy
0 = 2.165 + v2fy
v2fy = -2.165 m/s
Finding the Struck Ball’s Final Speed and Direction:
Now that we have the x and y components of the second ball’s final velocity (v2fx and v2fy), we can find its speed (magnitude) using the Pythagorean theorem and its direction using trigonometry.
Speed v2f = sqrt(v2fx² + v2fy²) = sqrt((1.25)² + (-2.165)²) = sqrt(1.5625 + 4.687225) = sqrt(6.25) = 2.50 m/s
Direction θ = arctan(v2fy / v2fx) = arctan(-2.165 / 1.25) = arctan(-1.732) = -60°
Answer for (a): The struck ball moves with a speed of 2.50 m/s at an angle of -60° (or 60° below the original line of motion).
b) Is the collision really elastic? Prove that.
A collision is elastic if the total kinetic energy of the system is conserved, meaning the total kinetic energy before the collision is equal to the total kinetic energy after the collision. We will calculate both values to verify this.
Initial Kinetic Energy (KEi):
Only the first ball is moving initially.
KEi = (1/2)m * v1i² + (1/2)m * v2i²
KEi = (1/2)m * (5.00)² + (1/2)m * (0)²
KEi = (1/2)m * 25 = 12.5m
Final Kinetic Energy (KEf):
Both balls are moving after the collision.
KEf = (1/2)m * v1f² + (1/2)m * v2f²
KEf = (1/2)m * (4.33)² + (1/2)m * (2.50)²
KEf = (1/2)m * (18.7489 + 6.25)
KEf = (1/2)m * (24.9989)
KEf ≈ 12.5m
Proof:
Comparing the initial and final kinetic energies, we find that KEi = 12.5m and KEf ≈ 12.5m. The very small difference is due to the rounding of the value 4.33 m/s in the problem statement (the exact value would be 5 * cos(30°) ≈ 4.3301 m/s). Within the precision of the given numbers, the kinetic energy is conserved.
Answer for (b): Yes, the collision is elastic because the total kinetic energy before the collision (12.5m) is equal to the total kinetic energy after the collision (approximately 12.5m).
