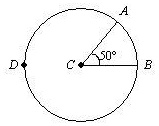
In the given figure, O is the center of the circle
The Correct Answer and Explanation is:
The correct answer is that the measure of arc AB is 50°.
This answer is derived from the definition of a central angle in a circle. The provided image shows a circle with its center at point C. The lines extending from the center C to the points A and B on the circle’s edge are radii. The angle formed between these two radii at the center of the circle, ∠ACB, is called a central angle. The problem states that the measure of this central angle is 50°.
In geometry, an arc is a continuous section of the circumference of a circle. The arc that lies in the interior of a central angle and connects the two points where the radii meet the circle is known as the intercepted arc. In this figure, arc AB is the intercepted arc for the central angle ∠ACB.
A core theorem of circle geometry states that the measure of a central angle is equal to the measure of its intercepted arc. This relationship is a direct one to one correspondence. Since the full circle comprises 360 degrees, the measure of an arc represents its proportional part of the entire circle. Therefore, because the central angle ∠ACB is given as 50°, the measure of the arc it intercepts, arc AB, is also 50°.
This measure is an angular value in degrees, not a linear measurement of length. To find the actual length of arc AB, one would need additional information, specifically the length of the circle’s radius. The image also includes a point D on the circle, but its position is not defined by any angles, so we cannot determine the measure of arcs associated with it, such as arc AD or arc BD, from the given information alone.
