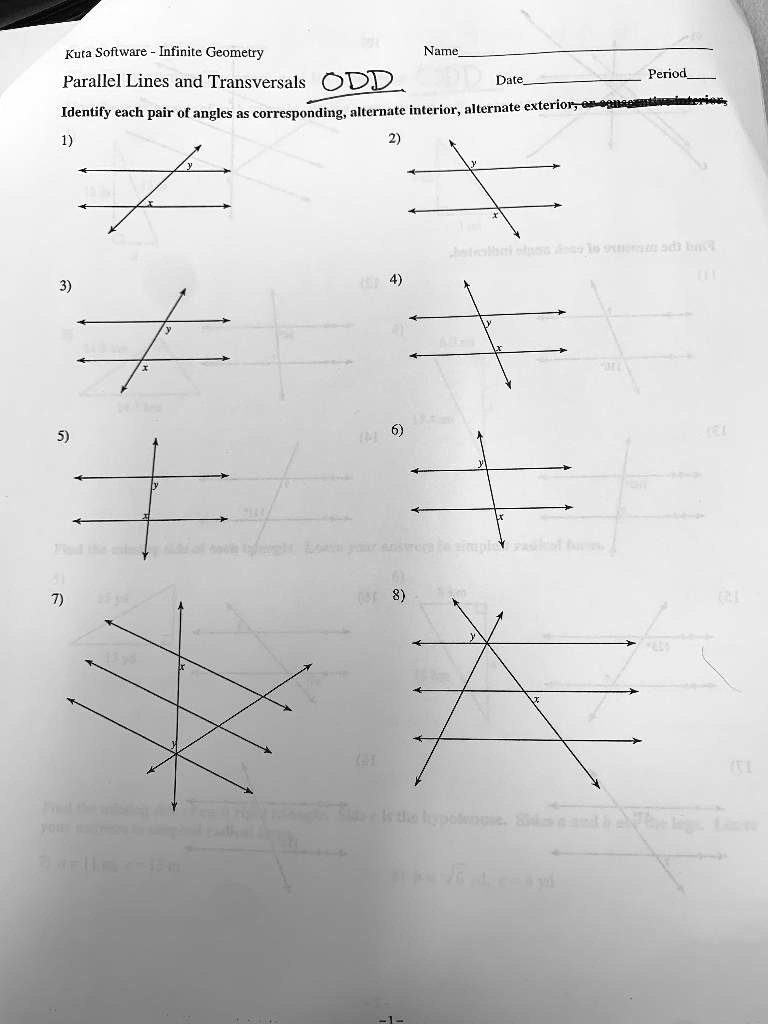
Kuta Software Infinite Geometry Name: Parallel Lines and Transversals ODD Date: Identify each pair of angles as corresponding, alternate interior, or alternate exterior.
The Correct Answer and Explanation is:
Based on the odd-numbered problems in the provided geometry worksheet, here are the correct answers and a detailed explanation.
Answers:
- Corresponding angles
- Alternate interior angles
- Consecutive interior angles (also known as same-side interior angles)
- No relationship
Explanation
This worksheet focuses on identifying the relationships between angles created when a transversal line intersects two or more parallel lines. Understanding the terminology is key to correctly identifying each pair. The area between the two parallel lines is called the interior region, and the areas outside the parallel lines are the exterior regions.
1. Corresponding Angles:
In problem 1, angles x and y are classified as corresponding angles. This is because they are in the same relative position at each intersection point. Imagine sliding the top parallel line and its intersection point down along the transversal until it rests on top of the bottom intersection. Angle y would perfectly overlap with angle x. Both angles are located in the bottom left position relative to their respective intersections. When the lines are parallel, as they are here, corresponding angles are always congruent, meaning they have the same measure.
3. Alternate Interior Angles:
In problem 3, the pair of angles x and y are alternate interior angles. The term “interior” signifies that both angles lie in the region between the two parallel lines. The term “alternate” means they are on opposite sides of the transversal. Angle y is in the interior and on the right side of the transversal, while angle x is also in the interior but on the left side. Because they are on opposite sides of the transversal and between the parallel lines, they fit this definition. For parallel lines, alternate interior angles are also congruent.
5. Consecutive Interior Angles:
Problem 5 shows a pair of angles, x and y, that are consecutive interior angles. This term, also known as same side interior angles, was likely the fourth option cut off in the worksheet’s instructions. Both angles are “interior” because they are located between the parallel lines. They are “consecutive” or “same side” because they both lie on the same side of the transversal, which in this case is the right side. Unlike the previous angle pairs, consecutive interior angles are not congruent; instead, they are supplementary, meaning their measures add up to 180 degrees when the lines are parallel.
7. No Relationship:
The angles x and y in problem 7 do not have one of the defined relationships. All the standard angle-pair classifications like corresponding, alternate interior, or consecutive interior depend on the two angles being formed by the same transversal. In this diagram, there are two different transversals intersecting the parallel lines. Angle x is formed by the vertical transversal, while angle y is formed by the diagonal transversal. Since they do not share a common transversal, we cannot directly classify their relationship using these geometric terms.
