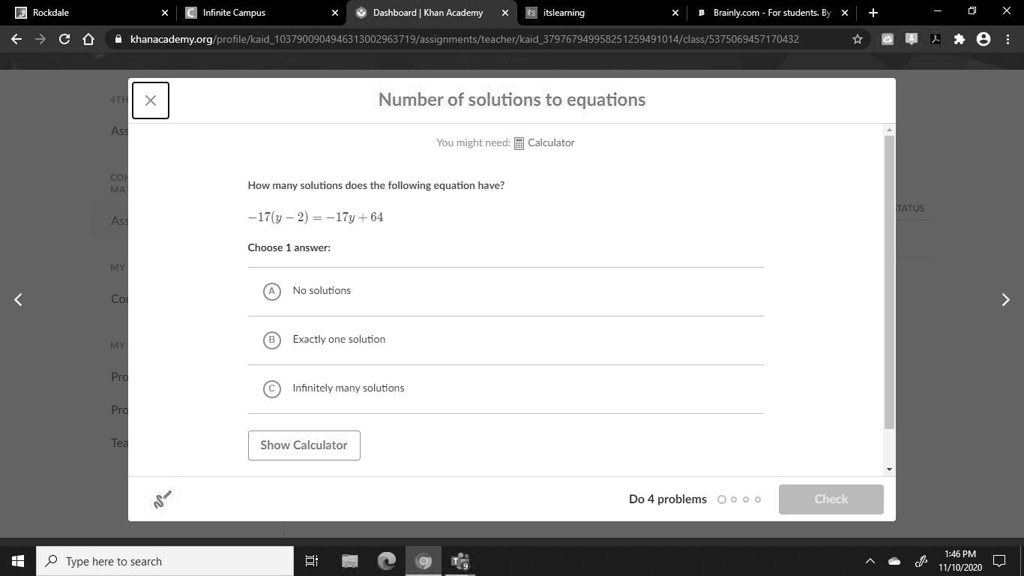
Number of solutions to equations You might need: Calculator How many solutions does the following equation have?
Choose 1 answer: A No solutions B Exactly one solution C Infinitely many solutions Show Calculator Do 4 problems Check
The Correct Answer and Explanation is:
The correct answer is A) No solutions.
To determine the number of solutions for the equation -17(y – 2) = -17y + 64, we need to simplify it and attempt to solve for the variable y.
First, we simplify the left side of the equation by applying the distributive property. This means we multiply -17 by each term inside the parentheses:
-17 * y = -17y
-17 * (-2) = +34
Now, we can rewrite the equation with the simplified left side:
-17y + 34 = -17y + 64
Next, our goal is to isolate the variable y. We can begin by trying to gather all the terms containing y on one side of the equation. A good way to do this is to add 17y to both sides:
(-17y + 34) + 17y = (-17y + 64) + 17y
On the left side, -17y and +17y cancel each other out, leaving just 34. Similarly, on the right side, -17y and +17y also cancel out, leaving 64. The equation now becomes:
34 = 64
This final statement, 34 = 64, is a contradiction. It is mathematically false. When solving an algebraic equation, if the variable terms are eliminated and the resulting statement is false, it indicates that there is no value of y that can ever make the original equation true. No matter what number you substitute for y, you will always end up with this false conclusion. Therefore, the equation has no solutions.
For comparison, if we had ended with a true statement like 34 = 34, there would be infinitely many solutions. If we had solved for a specific value, such as y = 5, there would be exactly one solution. Since we arrived at a contradiction, the correct choice is no solutions.
