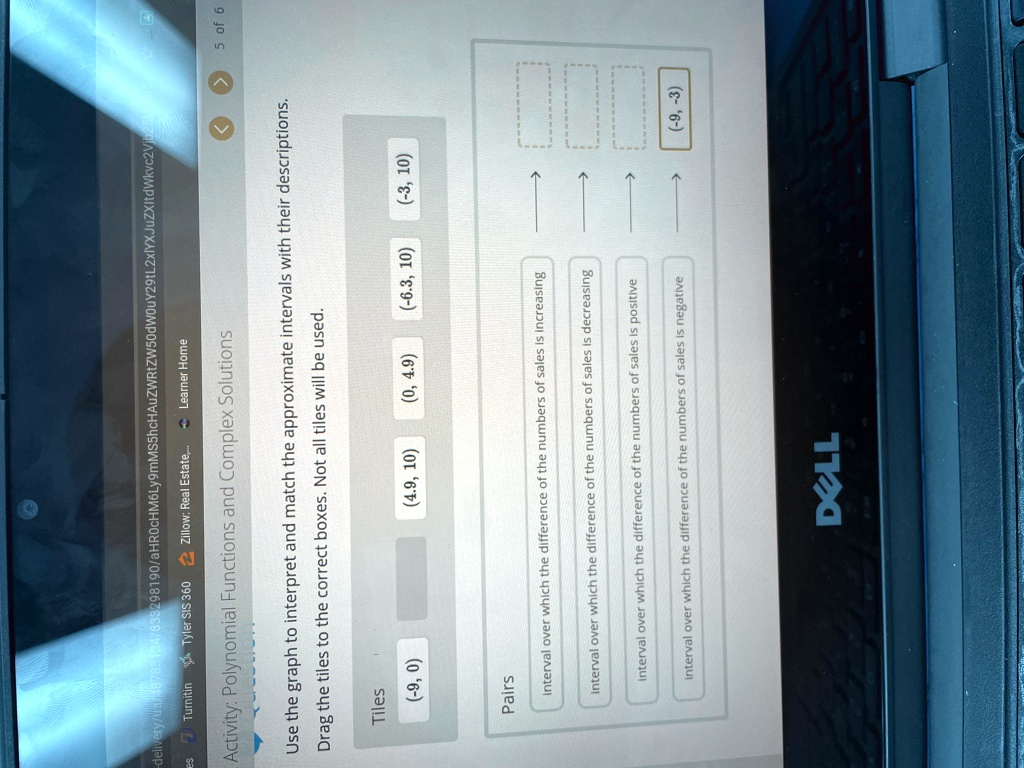
Polynomial Functions and Complex Solutions Use the graph to interpret and match the approximate intervals with their descriptions. Drag the tiles to the correct boxes. Not all tiles will be used. Tiles (-9, 0) (4.9, 10) (0, 4.9) (-6.3, 10) (-3, 10) Pairs Interval over which the difference of the numbers of sales is increasing Interval over which the difference of the numbers of sales is decreasing Interval over which the difference of the numbers of sales is positive Interval over which the difference of the numbers of sales is negative (-9, -3)
The Correct Answer and Explanation is:1
Based on the provided image, a definitive answer cannot be given because the graph, which is essential for solving this problem, is not visible. The instructions explicitly state, “Use the graph to interpret and match the approximate intervals with their descriptions.” However, I can explain the process you should follow to find the correct answer once you can see the graph.
The problem asks you to analyze a function that represents “the difference of the numbers of sales.” Think of this as the y-value on a graph. The intervals represent ranges along the x-axis.
Here is how to determine each match:
1. Interval over which the function is increasing:
An interval is increasing if the graph is going up as you read it from left to right. On the graph, find the section where the curve rises. The x-values that correspond to this upward slope make up the interval of increase. You would look for a part of the graph between a valley (a local minimum) and a peak (a local maximum).
2. Interval over which the function is decreasing:
An interval is decreasing if the graph is going down as you read it from left to right. You need to locate the part of the graph that has a downward slope. The x-values for this section are the interval of decrease. This typically occurs between a peak and a subsequent valley.
3. Interval over which the function is positive:
An interval is positive when the function’s graph is located entirely above the horizontal x-axis. For every x-value in this interval, the corresponding y-value will be greater than zero.
4. Interval over which the function is negative:
An interval is negative when the function’s graph is located entirely below the horizontal x-axis. For every x-value in this interval, the corresponding y-value will be less than zero. The image shows this has already been matched to (-9, -3). This tells you that on the missing graph, the curve is below the x-axis between x = -9 and x = -3.
To solve the problem, you must visually inspect your graph and apply these definitions to find which of the available tiles like (4.9, 10), (0, 4.9), or (-6.3, 10) correctly describe the graph’s behavior for the remaining categories.
