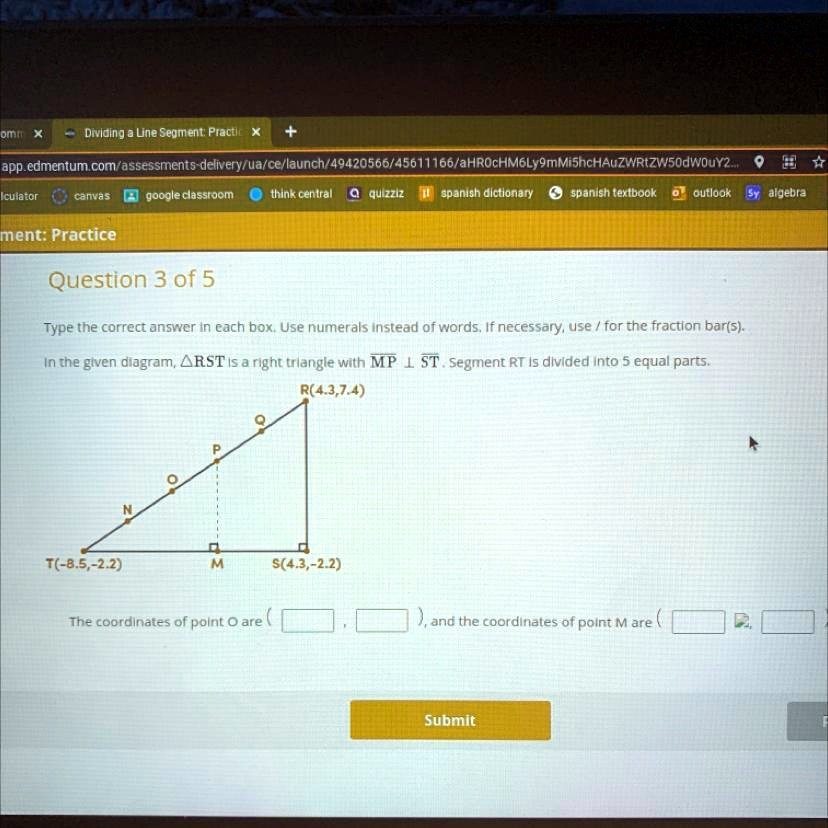
Type the correct answer in each box. Use numerals instead of words. If necessary, use / for the fraction bar(s). In the given diagram,
is a right triangle with
. Segment RT is divided into 5 equal parts. R(4.3, 7.4) T(-8.5, -2.2) S(4.3, -2.2) The coordinates of point O are ( , ), and the coordinates of point M are ( , )
The Correct Answer and Explanation is:
- R(4.3, 7.4)
- T(-8.5, -2.2)
- S(4.3, -2.2)
Step 1: Find the coordinates of point O.
From the image, we see that segment RT is divided into 5 equal parts. To find the coordinates of point O, we need to find the point that divides RT into these five equal segments.
We can use the section formula to divide the segment in a ratio. Since point O is the first point dividing RT, this is the 1st point, and the ratio is 1:4. The section formula for dividing a line segment between two points (x₁, y₁) and (x₂, y₂) in the ratio m:n is: x=nx1+mx2m+n,y=ny1+my2m+nx = \frac{n x_1 + m x_2}{m + n}, \quad y = \frac{n y_1 + m y_2}{m + n}x=m+nnx1+mx2,y=m+nny1+my2
Using the given coordinates for points R and T:
- m=1,n=4m = 1, n = 4m=1,n=4
- x1=4.3,y1=7.4x_1 = 4.3, y_1 = 7.4×1=4.3,y1=7.4
- x2=−8.5,y2=−2.2x_2 = -8.5, y_2 = -2.2×2=−8.5,y2=−2.2
Now, applying the formula: xO=4(4.3)+1(−8.5)4+1=17.2−8.55=8.75=1.74x_O = \frac{4(4.3) + 1(-8.5)}{4 + 1} = \frac{17.2 – 8.5}{5} = \frac{8.7}{5} = 1.74xO=4+14(4.3)+1(−8.5)=517.2−8.5=58.7=1.74 yO=4(7.4)+1(−2.2)4+1=29.6−2.25=27.45=5.48y_O = \frac{4(7.4) + 1(-2.2)}{4 + 1} = \frac{29.6 – 2.2}{5} = \frac{27.4}{5} = 5.48yO=4+14(7.4)+1(−2.2)=529.6−2.2=527.4=5.48
Thus, the coordinates of point O are (1.74, 5.48).
Step 2: Find the coordinates of point M.
Point M is the midpoint of segment RT. We can use the midpoint formula: xM=xR+xT2,yM=yR+yT2x_M = \frac{x_R + x_T}{2}, \quad y_M = \frac{y_R + y_T}{2}xM=2xR+xT,yM=2yR+yT
Substituting the coordinates of R and T: xM=4.3+(−8.5)2=−4.22=−2.1x_M = \frac{4.3 + (-8.5)}{2} = \frac{-4.2}{2} = -2.1xM=24.3+(−8.5)=2−4.2=−2.1 yM=7.4+(−2.2)2=5.22=2.6y_M = \frac{7.4 + (-2.2)}{2} = \frac{5.2}{2} = 2.6yM=27.4+(−2.2)=25.2=2.6
Thus, the coordinates of point M are (-2.1, 2.6).
Final Answer:
- Coordinates of point O: (1.74, 5.48)
- Coordinates of point M: (-2.1, 2.6)
