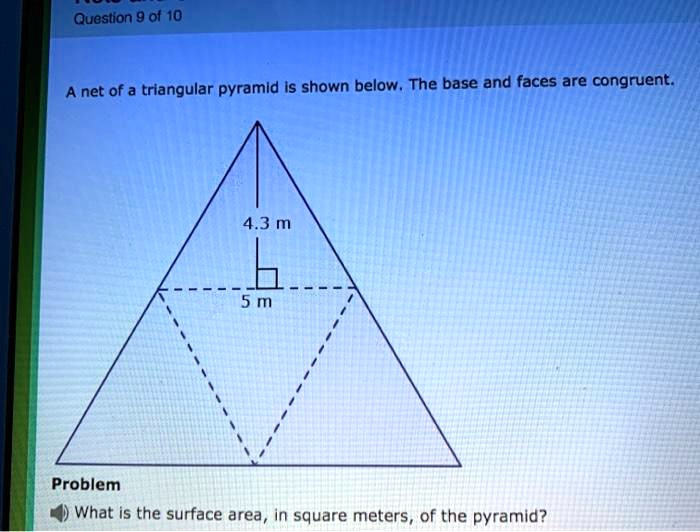
A net of a triangular pyramid is shown below. The base and faces are congruent. 4.3 m 5 m Problem What is the surface area, in square meters, of the pyramid?
The Correct Answer and Explanation is:
The correct surface area of the pyramid is 43 square meters.
Here is a detailed explanation of how to arrive at this answer.
The problem asks for the total surface area of a triangular pyramid. The image provided shows the pyramid’s net, which is the flat pattern you get if you unfold the three dimensional shape. The surface area is the sum of the areas of all the individual shapes that make up this net.
First, we need to identify the shapes in the net. A triangular pyramid consists of one triangular base and three triangular faces. This means the net is composed of a total of four triangles. The problem statement provides a crucial piece of information: “The base and faces are congruent.” This tells us that all four triangles are identical in size and shape. Therefore, we only need to calculate the area of one triangle and then multiply it by four to find the total surface area.
The formula for the area of a single triangle is:
Area = (1/2) * base * height
From the image, we are given the dimensions for one of these congruent triangles:
The base of the triangle is 5 meters.
The height of the triangle is 4.3 meters.
Now, we can substitute these values into the area formula:
Area of one triangle = (1/2) * 5 m * 4.3 m
Area of one triangle = 0.5 * 21.5 sq m
Area of one triangle = 10.75 square meters
Since the pyramid is made of four of these identical triangles, we find the total surface area by multiplying the area of one triangle by four:
Total Surface Area = Area of one triangle * 4
Total Surface Area = 10.75 sq m * 4
Total Surface Area = 43 square meters
Thus, the total surface area of the pyramid is 43 square meters.
