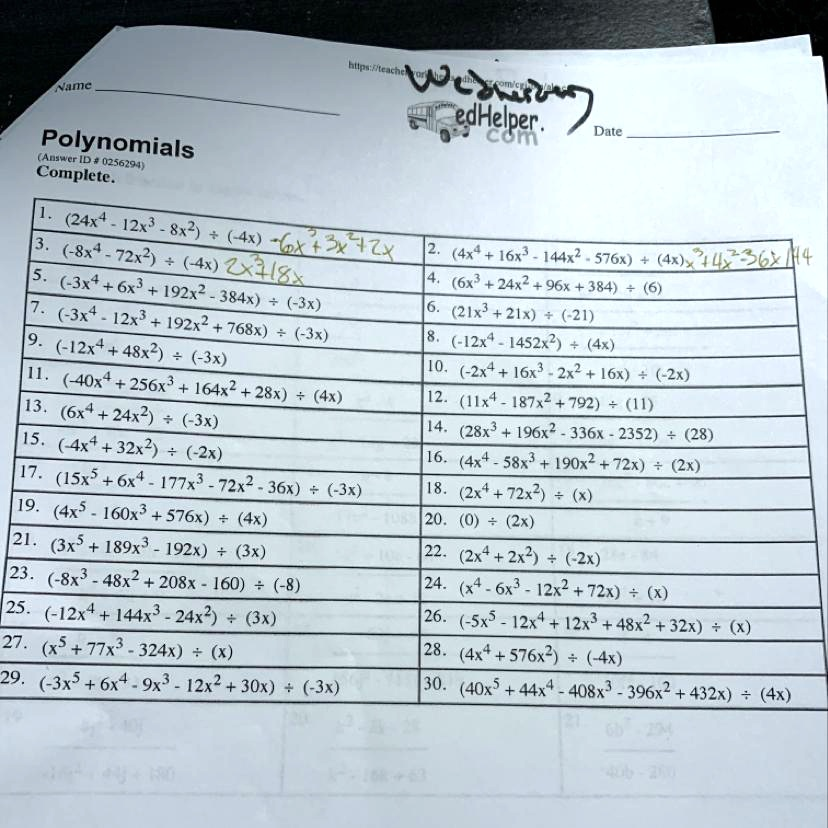
Please help me solve this!!! Vumc Polynomials (Answer ID # 02562741 Complete. huna”f eacne VcccD SedHelper; Date (24x^4 + 12x^3 + 8x^2) (4x) (-8x^4 + 72x^2) (AA4x) (4x + 16r` + 144x^2 + 576x) (Ax)y 74261 21ls (3x^2 + 6x^3 + 192x^2 + (6x^3 + 24x^2 + 96x + 384) 384x) (-3x) (-3x^4 + 12x^3 + (2Ix^3 + 21x) 192x^2 + (-21) 7681) (-x) (-12x+ (-12x^4 + 48x^2) [452x^2) (-3x) I1_ 10 (-2x^4 + 16x^8 + (40x+ + 256x^3 + 2x^2 + [6x) (-Zx) 164x^2 + 28x) 13 . (4x) (Ix^4 – 187x^2 + 792) (6x! + 24x^2) (11) (-3x) 15 . (28x’ + 196x? _ 336x 2352) + (28) (-4xt +32x^2) (-2x) 16 . (4x^4 – 58x^3 + [90x^2 + 17 72x) (2x) (ISx^5 + 6x^4 177x^3 72x^2 36x) (-3x) 18 (2x+ 72x^2) 19. (4x^5 160x^2 + 576x) (4x) 20 . (0) (2x) 121. (3x^5 + 189x^3 192x) (3x) 22 (Zx 2x^2) (~Zx) 23 (-8x^2 _ 48x^2 + 208x 160) (-8) 24 6x^3 12x^2 + 72x) 25. (-12x^4 + 144x^3 _ 24x^2) (3x) 26 . (-Sx^2 12x’ + 12x^2 + 48x^2 + 32x) (X) 27. 77x^3 324x) 28 (4x^4+ 576x^2) (-4x) 29 (-3x^5 + 6x^4 9x^2 – 12x^2 + 30x) (-3x) 30 (40x^5 + 44x^4 _ 408x^3 396x^2 + 432x) (4x)
The Correct Answer and Explanation is:
Of course. Here is the solution to the polynomial division problems on the worksheet, along with a detailed explanation of the process.
Explanation of the Method
This worksheet involves dividing a polynomial (an expression with multiple terms) by a monomial (an expression with a single term). The fundamental rule for this operation is straightforward: you must divide each individual term of the polynomial by the monomial divisor.
This process involves two main steps for each term:
- Divide the Coefficients: Divide the number part of the term in the polynomial by the number part of the monomial. Pay close attention to the signs; for example, a negative number divided by a negative number results in a positive number.
- Divide the Variables: Divide the variable parts using the rules of exponents. When dividing variables with the same base, you subtract the exponents. For instance, x⁵ ÷ x² = x^(5-2) = x³. Remember that a variable with no visible exponent, like x, is considered to have an exponent of 1 (x¹).
Let’s walk through a few examples from your worksheet.
Example: Problem 1
(24x⁴ – 12x³ – 8x²) ÷ (-4x)
We divide each term by -4x:
- First term: (24x⁴) ÷ (-4x). Divide the coefficients: 24 ÷ (-4) = -6. Divide the variables: x⁴ ÷ x¹ = x³. The result is -6x³.
- Second term: (-12x³) ÷ (-4x). Divide the coefficients: -12 ÷ (-4) = +3. Divide the variables: x³ ÷ x¹ = x². The result is +3x².
- Third term: (-8x²) ÷ (-4x). Divide the coefficients: -8 ÷ (-4) = +2. Divide the variables: x² ÷ x¹ = x¹. The result is +2x.
Combining these results gives the final answer: -6x³ + 3x² + 2x.
Example: Problem 23
(-8x³ – 48x² + 208x – 160) ÷ (-8)
Here, the divisor is just a constant. The principle remains the same.
- (-8x³) ÷ (-8) = x³
- (-48x²) ÷ (-8) = +6x²
- (208x) ÷ (-8) = -26x
- (-160) ÷ (-8) = +20
The final answer is: x³ + 6x² – 26x + 20.
Correct Answers
Here are the complete answers for all the problems on the worksheet.
- -6x³ + 3x² + 2x
- x³ + 4x² – 36x – 144
- 2x³ + 18x
- x³ + 4x² + 16x + 64
- x³ – 2x² – 64x + 128
- -x² – 1
- x³ – 4x² – 64x – 256
- 3x³ + 363x
- 4x³ – 16x
- x³ – 8x² + x – 8
- -10x³ + 64x² + 41x + 7
- x³ – 17x + 72
- -2x³ – 8x
- x³ + 7x² – 12x – 84
- 2x³ – 16x
- 2x³ – 29x² + 95x + 36
- -5x⁴ – 2x³ + 59x² + 24x + 12
- 2x³ + 72x
- x⁴ – 40x² + 144
- 0
- x⁴ + 63x² – 64
- -x³ – x
- x³ + 6x² – 26x + 20
- x³ – 6x² – 12x + 72
- -4x³ + 48x² – 8x
- -5x⁴ – 12x³ + 12x² + 48x + 32
- x⁴ + 77x² – 324
- -x³ – 144x
- x⁴ – 2x³ + 3x² + 4x – 10
- 10x⁴ + 11x³ – 102x² – 99x + 108
