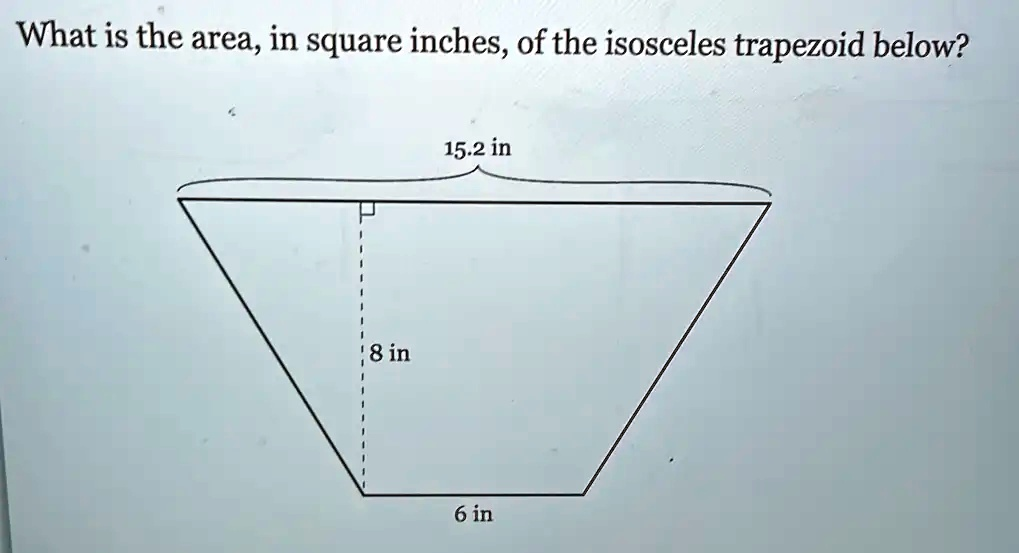
What is the area, in square inches, of the isosceles trapezoid below? 15.2 in 8 in 6 in
The Correct Answer and Explanation is:
The correct area of the isosceles trapezoid is 84.8 square inches.
To determine the area of any trapezoid, including an isosceles one, you can use the standard mathematical formula. The formula for the area of a trapezoid is:
Area = [(base1 + base2) / 2] * height
This formula essentially calculates the average length of the two parallel bases and then multiplies it by the perpendicular height. Let’s identify each of these values from the image provided.
The two parallel sides of the trapezoid are its bases. In the diagram, these are the top and bottom horizontal lines.
- The longer base (let’s call it b1) is given as 15.2 inches.
- The shorter base (let’s call it b2) is given as 6 inches.
- The height (h) is the perpendicular distance between these two bases. The diagram shows this with a dashed line and a right-angle symbol, indicating its value is 8 inches.
Now we can substitute these values directly into the area formula.
First, we add the lengths of the two bases:
Sum of bases = 15.2 in + 6 in = 21.2 in
Next, we take the average of these bases by dividing their sum by 2:
Average of bases = 21.2 in / 2 = 10.6 in
Finally, we multiply this average base length by the height to find the total area:
Area = 10.6 in * 8 in = 84.8 square inches
The information that the trapezoid is “isosceles” means its non-parallel sides are equal in length, but this fact is not needed for the area calculation since the height was already provided. The calculation relies only on the lengths of the two bases and the perpendicular height. Thus, the final calculated area of the given trapezoid is 84.8 square inches.
