If ∠ and ∠ are complementary angles, then one of them must have a measure less than 45°.
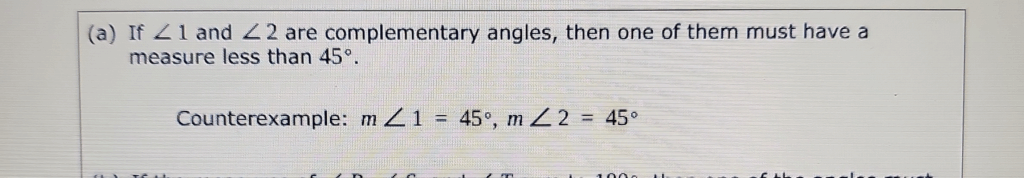
The Correct Answer and Explanation is:
The counterexample provided in the image is correct. It successfully proves that the original statement is false.
Here is an explanation:
The original statement is a conditional statement: “If ∠1 and ∠2 are complementary angles, then one of them must have a measure less than 45°.” To determine if this statement is true or false, we can test it with a counterexample. A counterexample is a specific instance that satisfies the first part of the statement (the “if” clause) but does not satisfy the second part (the “then” clause).
First, let’s define the terms. Complementary angles are a pair of angles whose measures add up to exactly 90 degrees. The “if” clause of the statement requires that m∠1 + m∠2 = 90°. The “then” clause claims that as a result, either m∠1 must be less than 45° or m∠2 must be less than 45°.
Now, let’s examine the proposed counterexample: m∠1 = 45° and m∠2 = 45°.
We must first check if this example meets the condition of the “if” clause. Are the angles complementary? We can check by adding their measures: 45° + 45° = 90°. Since their sum is 90°, they are indeed complementary angles. This means the first part of the statement is satisfied.
Next, we evaluate the “then” clause using this example. The clause states that one of the angles must be less than 45°. In our example, neither angle is less than 45°. Both are exactly equal to 45°. Because the condition that one angle must be less than 45° is not met, the “then” clause is false for this specific case.
Since we have found an example that fulfills the initial condition but falsifies the conclusion, the original statement is proven to be false. The counterexample correctly identifies the single scenario where the statement fails. While for most complementary pairs one angle is indeed less than 45° (for instance, 30° and 60°), the existence of this one exception is enough to invalidate the absolute certainty of the word “must” in the statement.
