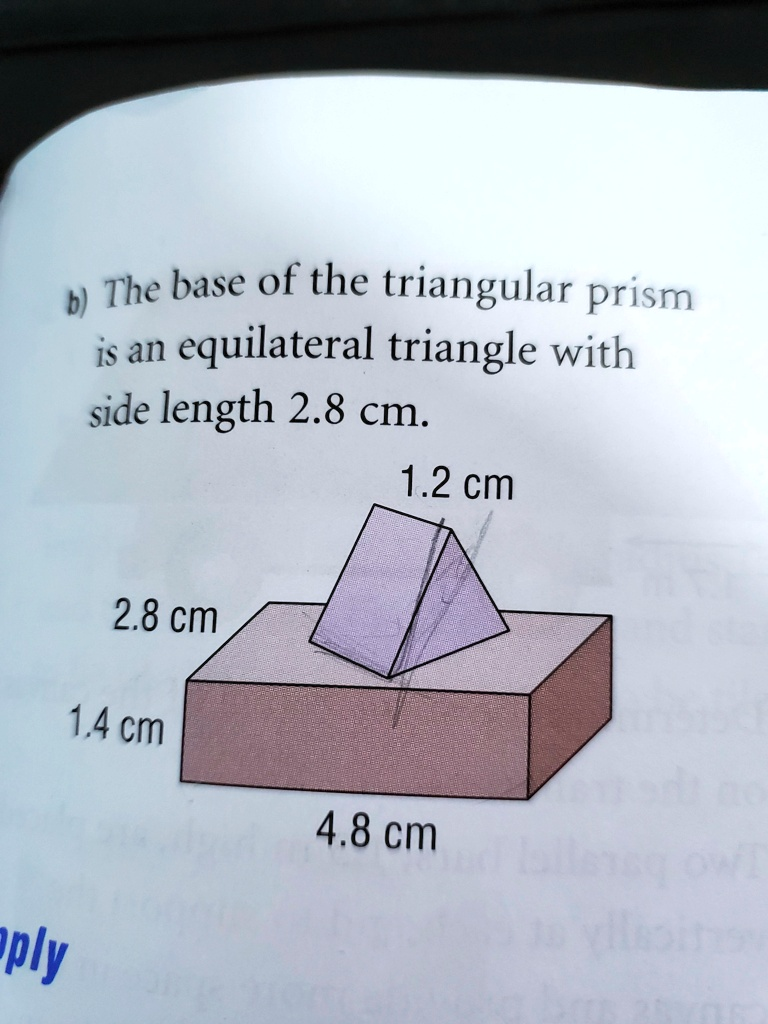
The base of the triangular prism is an equilateral triangle with side length 2.8 cm. 2.8 cm 1.4 cm 1.2 cm 4.8 cm
The Correct Answer and Explanation is:
Based on the provided image and geometric principles, the correct answer is the total volume of the composite solid.
Correct Answer: 22.90 cm³
Explanation
The image displays a composite 3D shape, which consists of a rectangular prism at the bottom and a triangular prism on top. To find the total volume of this object, we must calculate the volume of each individual shape and then add them together.
First, we calculate the volume of the rectangular prism. The formula for the volume of a rectangular prism is Volume = Length × Width × Height. According to the diagram, the dimensions are a length of 4.8 cm, a width of 2.8 cm, and a height of 1.4 cm.
Volume of rectangular prism = 4.8 cm × 2.8 cm × 1.4 cm = 18.816 cm³.
Next, we calculate the volume of the triangular prism. The formula for its volume is Volume = Area of the base × Height of the prism. The text specifies that the base is an equilateral triangle with a side length of 2.8 cm. The area of an equilateral triangle is found using the formula Area = (s²√3) / 4, where ‘s’ is the side length.
Area of the triangular base = (2.8² × √3) / 4
Area = (7.84 × √3) / 4 ≈ 3.395 cm².
The height (or length) of the triangular prism, which is the distance between its two triangular faces, is given as 1.2 cm.
Volume of triangular prism = 3.395 cm² × 1.2 cm ≈ 4.074 cm³.
Finally, to find the total volume of the entire object, we sum the volumes of the two component shapes.
Total Volume = Volume of rectangular prism + Volume of triangular prism
Total Volume = 18.816 cm³ + 4.074 cm³ = 22.89 cm³.
Rounding the final result to two decimal places gives a total volume of 22.90 cm³.
