The Correct Answer and Explanation is:
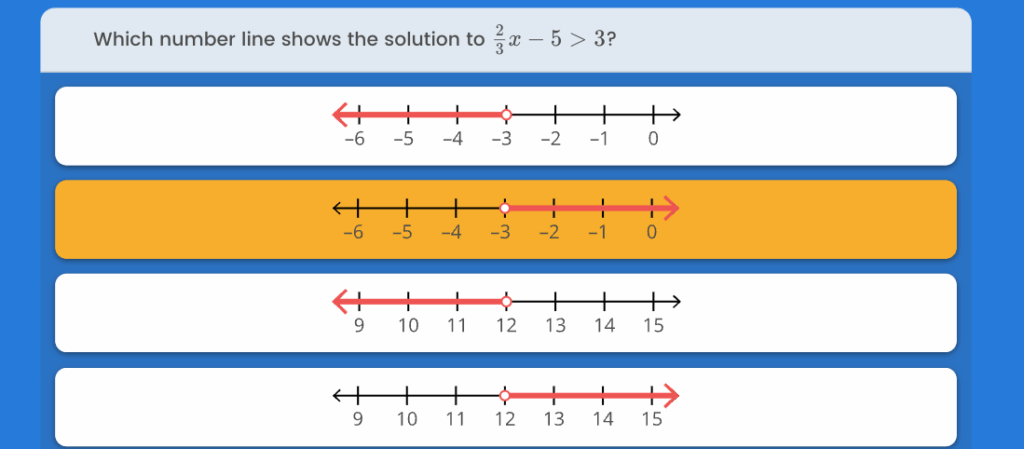
The correct answer is the fourth number line shown in the image.
To determine the correct number line, we must first solve the inequality (2/3)x – 5 > 3. The objective is to isolate the variable x.
- Add 5 to both sides: The first step is to eliminate the constant term (-5) on the left side of the inequality. We do this by adding 5 to both sides to maintain the inequality’s balance.
(2/3)x – 5 + 5 > 3 + 5
(2/3)x > 8 - Multiply by the reciprocal: Now, to isolate x, we need to remove the coefficient 2/3. We can achieve this by multiplying both sides of the inequality by the reciprocal of 2/3, which is 3/2. Because we are multiplying by a positive number, the direction of the inequality sign remains the same.
(3/2) * (2/3)x > 8 * (3/2)
x > 24 / 2
x > 12
The solution to the inequality is x > 12. This means that any number greater than 12 is a solution.
Now, we need to find the number line that represents this solution. The graphical representation of x > 12 has two important features:
- An open circle: The inequality is “greater than” (>), not “greater than or equal to” (≥). This signifies that 12 is the boundary but is not included in the solution set. This is shown on a number line with an open, or hollow, circle at 12.
- An arrow to the right: The solution includes all numbers that are larger than 12. Therefore, the number line must be shaded to the right of 12, with an arrow pointing towards the larger values (13, 14, 15, and so on) to indicate that the solution continues to infinity.
Analyzing the options:
- The first number line shows x < -3.
- The second number line shows x > -3.
- The third number line shows x < 12.
- The fourth number line shows an open circle at 12 and an arrow pointing to the right.
The fourth number line is the only one that correctly represents the solution x > 12.
