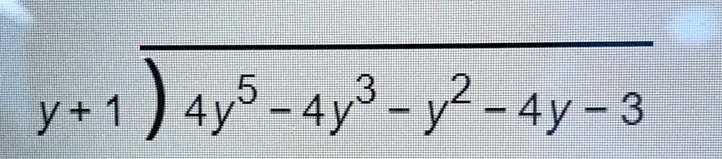
The Correct Answer and Explanation is:
The correct answer is 4y⁴ – 4y³ – y – 3.
This problem is solved using polynomial long division. The goal is to divide the dividend, 4y⁵ – 4y³ – y² – 4y – 3, by the divisor, y + 1.
First, we set up the division. It is crucial to account for all powers of the variable y in descending order in the dividend. The dividend is missing a term with y⁴, so we insert a placeholder, 0y⁴, to maintain proper column alignment. The dividend is written as 4y⁵ + 0y⁴ – 4y³ – y² – 4y – 3.
The process begins by dividing the first term of the dividend, 4y⁵, by the first term of the divisor, y. The result is 4y⁴, which becomes the first term of our quotient. We then multiply this 4y⁴ by the entire divisor (y + 1) to get 4y⁵ + 4y⁴. This result is placed below the dividend and subtracted. The subtraction (4y⁵ + 0y⁴) – (4y⁵ + 4y⁴) yields –4y⁴. We then bring down the next term from the dividend, –4y³, to get a new expression: –4y⁴ – 4y³.
Next, we repeat the process. We divide the first term of this new expression, –4y⁴, by the first term of the divisor, y, which gives us –4y³. This is the second term of our quotient. Multiplying –4y³ by the divisor (y + 1) gives –4y⁴ – 4y³. Subtracting this from the current line, (–4y⁴ – 4y³) – (–4y⁴ – 4y³), results in 0. We then bring down the next two terms, –y² and –4y.
Now, we divide –y² by y to get –y, the third term of the quotient. Multiplying –y by (y + 1) gives –y² – y. We subtract this from the current expression: (–y² – 4y) – (–y² – y) results in –3y. We bring down the final term, –3.
Finally, we divide –3y by y, which gives –3. This is the last term of our quotient. Multiplying –3 by (y + 1) gives –3y – 3. Subtracting this from the remaining expression (–3y – 3) results in a remainder of 0.
Since the remainder is 0, the division is exact. The final quotient is the polynomial we constructed on top: 4y⁴ – 4y³ – y – 3.
