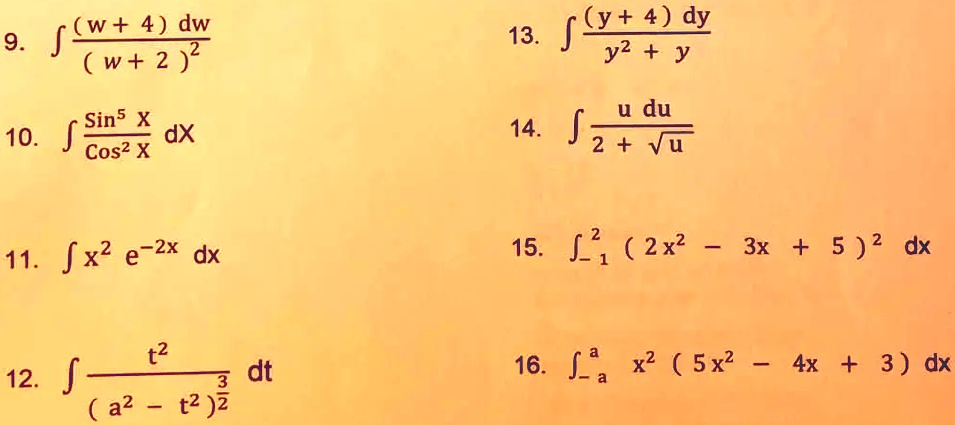
The Correct Answer and Explanation is:
Here is the solution and explanation for problem number 11 from the image.
Problem 11: ∫ x² e⁻²ˣ dx
Correct Answer: – (1/2)x²e⁻²ˣ – (1/2)xe⁻²ˣ – (1/4)e⁻²ˣ + C
Explanation:
This integral is best solved using the technique of integration by parts, which is applied when the integrand is a product of two different types of functions. The formula for integration by parts is ∫ u dv = uv – ∫ v du. The key to this method is choosing the parts u and dv correctly. A common guideline is the LIPET or LIATE rule (Logarithmic, Inverse Trig, Polynomial/Algebraic, Exponential/Trigonometric), which suggests the order for choosing u. In this case, we have a polynomial term (x²) and an exponential term (e⁻²ˣ), so we choose the polynomial as u.
For the first application of integration by parts:
Let u = x² and dv = e⁻²ˣ dx.
Then we find du by differentiating u, and v by integrating dv:
du = 2x dx
v = ∫ e⁻²ˣ dx = -1/2 e⁻²ˣ
Plugging these into the formula gives:
∫ x² e⁻²ˣ dx = (x²)(-1/2 e⁻²ˣ) – ∫ (-1/2 e⁻²ˣ)(2x dx)
= -1/2 x² e⁻²ˣ + ∫ x e⁻²ˣ dx
The new integral, ∫ x e⁻²ˣ dx, still requires integration by parts. We apply the process again:
Let u = x and dv = e⁻²ˣ dx.
Then du = dx and v = -1/2 e⁻²ˣ.
Applying the formula to this second integral:
∫ x e⁻²ˣ dx = (x)(-1/2 e⁻²ˣ) – ∫ (-1/2 e⁻²ˣ) dx
= -1/2 xe⁻²ˣ + 1/2 ∫ e⁻²ˣ dx
= -1/2 xe⁻²ˣ + 1/2 (-1/2 e⁻²ˣ)
= -1/2 xe⁻²ˣ – 1/4 e⁻²ˣ
Now, we substitute this result back into our first equation:
∫ x² e⁻²ˣ dx = -1/2 x² e⁻²ˣ + (-1/2 xe⁻²ˣ – 1/4 e⁻²ˣ)
Finally, we combine the terms and add the constant of integration, C, to get the final answer:
-1/2 x²e⁻²ˣ – 1/2 xe⁻²ˣ – 1/4 e⁻²ˣ + C
