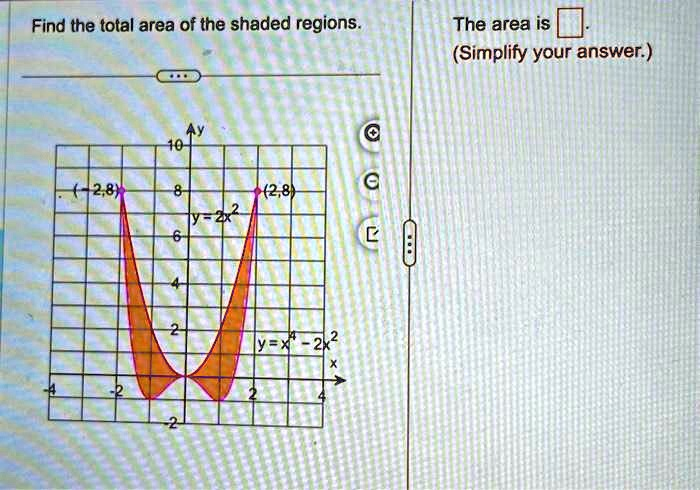
Find the total area of the shaded regions. Ay 10 (-2,8) 8 (2,8) y = 2x^2 6 4 2 y = x^4 – 2x^2 -4 -2 2 4 -2 The area is (Simplify your answer.)
The Correct Answer and Explanation is:
The correct answer is 128/15.
Explanation:
To determine the total area of the shaded regions, we need to calculate the definite integral representing the area between the two given curves: the upper curve y = 2x^2 and the lower curve y = x^4 – 2x^2.
1. Find the Limits of Integration
First, we find the points where the two curves intersect by setting their equations equal to each other. These intersection points will give us the limits of integration.
2x^2 = x^4 – 2x^2
0 = x^4 – 4x^2
Factor out x^2:
0 = x^2(x^2 – 4)
Factor the difference of squares (x^2 – 4):
0 = x^2(x – 2)(x + 2)
The solutions are x = 0, x = 2, and x = -2. These are the x-values that bound the shaded regions.
2. Set Up the Integral
The area between two curves is found by integrating the difference between the upper function and the lower function over the given interval. From the graph, y = 2x^2 is the upper curve and y = x^4 – 2x^2 is the lower curve across the entire shaded area, from x = -2 to x = 2.
The area (A) is given by the integral:
A = ∫[-2, 2] (upper curve – lower curve) dx
A = ∫[-2, 2] ( (2x^2) – (x^4 – 2x^2) ) dx
A = ∫[-2, 2] (4x^2 – x^4) dx
3. Use Symmetry to Simplify
Notice that the shaded area is symmetric with respect to the y-axis. The function we are integrating, f(x) = 4x^2 – x^4, is an even function because all powers of x are even. We can simplify the calculation by integrating from 0 to 2 and then multiplying the result by 2.
A = 2 * ∫[0, 2] (4x^2 – x^4) dx
4. Evaluate the Integral
First, find the antiderivative of the integrand:
∫(4x^2 – x^4) dx = 4(x^3/3) – (x^5/5) = (4/3)x^3 – (1/5)x^5
Now, apply the Fundamental Theorem of Calculus to evaluate the definite integral from 0 to 2:
A = 2 * [ (4/3)x^3 – (1/5)x^5 ] from 0 to 2
A = 2 * ( [ (4/3)(2)^3 – (1/5)(2)^5 ] – [ (4/3)(0)^3 – (1/5)(0)^5 ] )
A = 2 * ( [ (4/3)(8) – (1/5)(32) ] – 0 )
A = 2 * (32/3 – 32/5)
To subtract the fractions, find a common denominator (15):
A = 2 * ( (32 * 5)/(15) – (32 * 3)/(15) )
A = 2 * ( (160 – 96)/15 )
A = 2 * (64/15)
A = 128/15
The total area of the shaded regions is 128/15.
