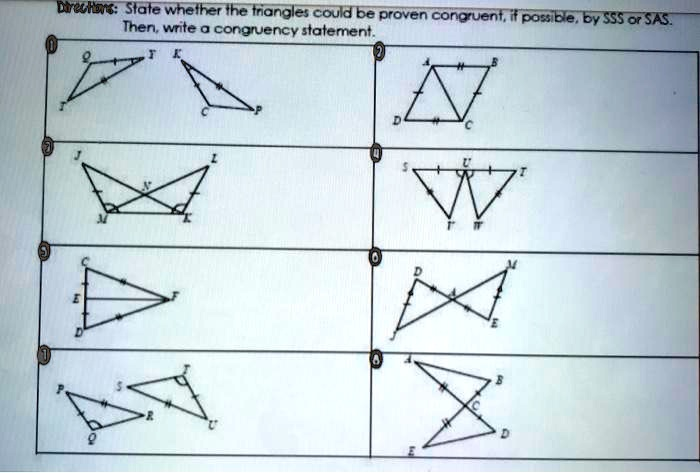
State whether the triangles could be proven congruent, if possible, by SSS or SAS. Then, write a congruency statement.
The Correct Answer and Explanation is:
Answers
- Triangles QOT and ECP
Congruent by SSS
Congruency Statement:
△QOT≅△ECP\triangle QOT \cong \triangle ECP△QOT≅△ECP - Triangles ADH and HBC
Congruent by SAS
Congruency Statement:
△ADH≅△HBC\triangle ADH \cong \triangle HBC△ADH≅△HBC - Triangles JKL and LMT
Congruent by SAS
Congruency Statement:
△JKL≅△LMT\triangle JKL \cong \triangle LMT△JKL≅△LMT - Triangles SUT and TUW
Congruent by SAS
Congruency Statement:
△SUT≅△TUW\triangle SUT \cong \triangle TUW△SUT≅△TUW - Triangles CEF and EDF
Congruent by SAS
Congruency Statement:
△CEF≅△EDF\triangle CEF \cong \triangle EDF△CEF≅△EDF - Triangles DAE and MEA
Congruent by SAS
Congruency Statement:
△DAE≅△MEA\triangle DAE \cong \triangle MEA△DAE≅△MEA - Triangles PQS and RUS
Congruent by SAS
Congruency Statement:
△PQS≅△RUS\triangle PQS \cong \triangle RUS△PQS≅△RUS - Triangles ACB and EDB
Congruent by SAS
Congruency Statement:
△ACB≅△EDB\triangle ACB \cong \triangle EDB△ACB≅△EDB
Explanation
To determine whether the triangles in each figure are congruent, we apply the congruence postulates SSS (Side-Side-Side) and SAS (Side-Angle-Side). These are valid when either all three sides are equal (SSS) or two sides and the included angle are equal (SAS).
In Figure 1, triangles QOT and ECP have three corresponding sides marked as equal. Therefore, by the SSS postulate, they are congruent.
In Figure 2, triangles ADH and HBC share a pair of equal sides and an included angle, with another pair of sides marked equal. This satisfies SAS.
Figure 3 shows triangles JKL and LMT with two pairs of equal sides and an included angle indicated by identical markings, proving SAS congruence.
Figure 4 has triangles SUT and TUW with equal sides on both ends of a shared angle. The vertical angle between the two triangles ensures the included angle is equal, so they are congruent by SAS.
Figure 5 compares triangles CEF and EDF. Both share a common side EF, and the other two sides are marked equal with the included angle, proving SAS congruence.
In Figure 6, triangles DAE and MEA share a common side AE and have two other corresponding sides equal, with the included angle equal, so SAS applies.
Figure 7 shows triangles PQS and RUS with two sides equal and the included angle indicated by markings, confirming SAS.
Finally, Figure 8 has triangles ACB and EDB sharing side AB and showing equal corresponding sides and included angle, making them congruent by SAS.
In conclusion, most cases are SAS since they rely on two equal sides and the included angle, while the first figure is SSS. These rules are fundamental in proving triangle congruence in geometry.
