Determine the value of x in the diagram below 2 5x + 55° 2x + 100° Show Your Work 2
The Correct Answer and Explanation is:1
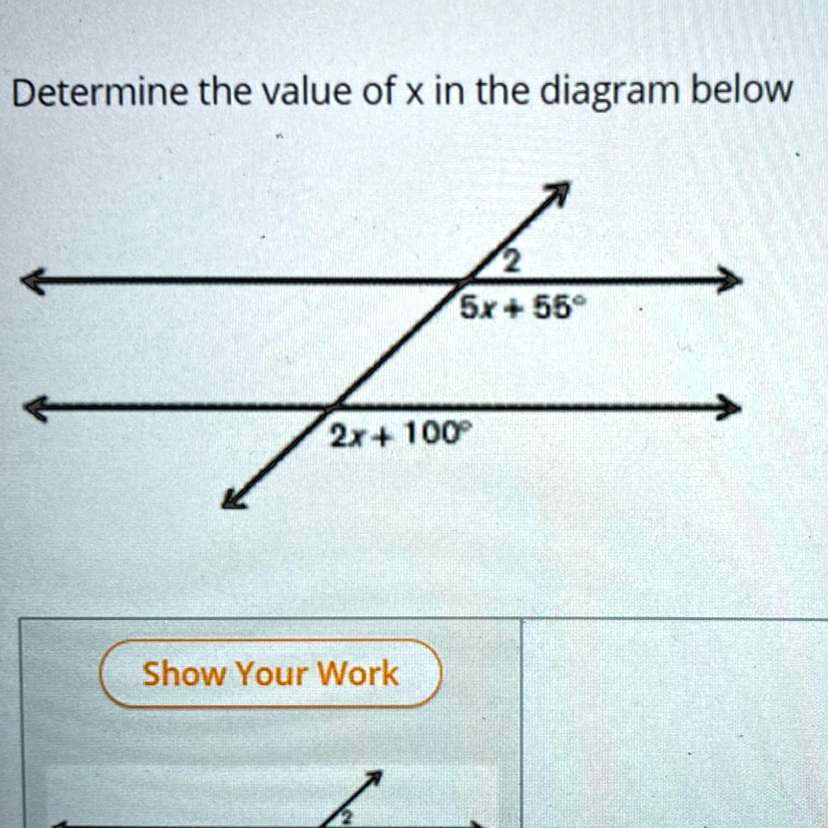
To determine the value of xxx in this problem, we need to rely on the fact that angles around a point or a line must add up to 180° or 360°, depending on the situation. In this case, we’re working with a pair of angles that form a linear pair.
You have two expressions for the angles:
- One angle: 5x+55∘5x + 55^\circ5x+55∘
- The other angle: 2x+100∘2x + 100^\circ2x+100∘
These two angles are supplementary (i.e., they add up to 180°), so we can set up an equation: (5x+55∘)+(2x+100∘)=180∘(5x + 55^\circ) + (2x + 100^\circ) = 180^\circ(5x+55∘)+(2x+100∘)=180∘
Step 1: Combine like terms
We’ll add the terms involving xxx and the constant terms together: 5x+2x+55∘+100∘=180∘5x + 2x + 55^\circ + 100^\circ = 180^\circ5x+2x+55∘+100∘=180∘ 7x+155∘=180∘7x + 155^\circ = 180^\circ7x+155∘=180∘
Step 2: Solve for xxx
Now, we’ll isolate xxx. First, subtract 155° from both sides: 7x=180∘−155∘7x = 180^\circ – 155^\circ7x=180∘−155∘ 7x=25∘7x = 25^\circ7x=25∘
Next, divide both sides by 7: x=25∘7x = \frac{25^\circ}{7}x=725∘ x≈3.57∘x \approx 3.57^\circx≈3.57∘
Conclusion:

The value of xxx is approximately 3.57∘3.57^\circ3.57∘.