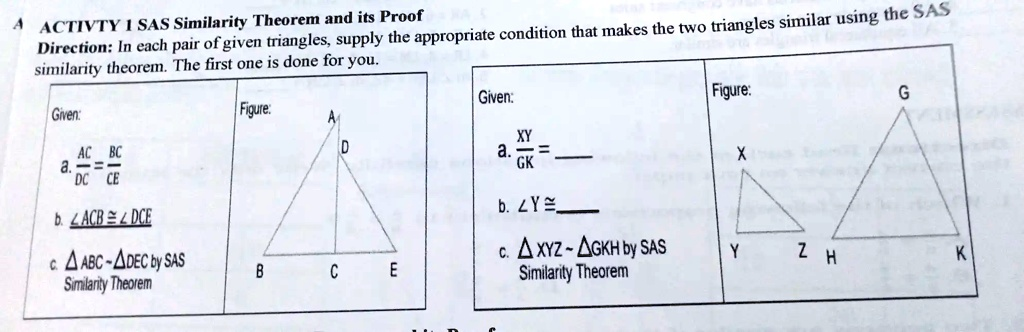
A ACTIVTY 1 SAS Similarity Theorem and its Proof Direction: In each pair of given triangles, supply the appropriate condition that makes the two triangles similar using the SAS similarity theorem. The first one is done for you. Given: AC BC a. \frac{AC}{DC} = \frac{BC}{CE} b. \angle ACB \cong \angle DCE c. \triangle ABC \sim \triangle DEC by SAS Similarity Theorem Figure: B C E Given: a. \frac{XY}{GK} = b. \angle Y \cong _ c. \triangle XYZ \sim \triangle GKH by SAS Similarity Theorem Figure: X G Y Z H K
The Correct Answer and Explanation is:
Of course. Here are the correct answers and a detailed explanation for the problem.
Correct Answers:
a. XY/GK = YZ/KH
b. ∠Y ≅ ∠K
Explanation
The problem requires you to complete the conditions necessary to prove that triangle XYZ is similar to triangle GKH using the Side-Angle-Side (SAS) Similarity Theorem. Let’s break down how to arrive at the correct answers.
Understanding the SAS Similarity Theorem
The SAS Similarity Theorem states that two triangles are similar if two pairs of corresponding sides are proportional, and their included angles are congruent. An “included angle” is the angle formed between the two sides being considered.
Analyzing the Given Information
The problem provides the final similarity statement: △XYZ ~ △GKH. This statement is the most crucial piece of information because it tells us exactly how the vertices of the two triangles correspond to each other:
- Vertex X corresponds to Vertex G.
- Vertex Y corresponds to Vertex K.
- Vertex Z corresponds to Vertex H.
This correspondence also dictates which angles and sides match up.
Solving for Blank b (The Angle)
Part (b) asks to complete the congruence statement ∠Y ≅ _____. This is the “Angle” part of the SAS theorem. Based on the correspondence established by △XYZ ~ △GKH, we know that angle Y in the first triangle corresponds to angle K in the second triangle. For the triangles to be similar by SAS, these included angles must be congruent. Therefore, the missing part is ∠K.
Solving for Blank a (The Side Proportions)
Part (a) deals with the “Side” proportions of the SAS theorem. We now know the included angles are ∠Y and ∠K. The sides that form these angles must be the ones used in the proportion.
- In △XYZ, the sides that form the included angle ∠Y are side XY and side YZ.
- In △GKH, the sides that form the included angle ∠K are side GK and side KH.
The problem gives the first part of the proportion as XY/GK. This correctly compares a pair of corresponding sides (XY and GK). To complete the proportion for the SAS theorem, we must use the other pair of corresponding sides that form the included angle. These are side YZ from the first triangle and side KH from the second triangle.
Thus, the complete proportion is XY/GK = YZ/KH. This fulfills the “Side-Side” requirement, showing that the two pairs of sides forming the included angle are proportional.
