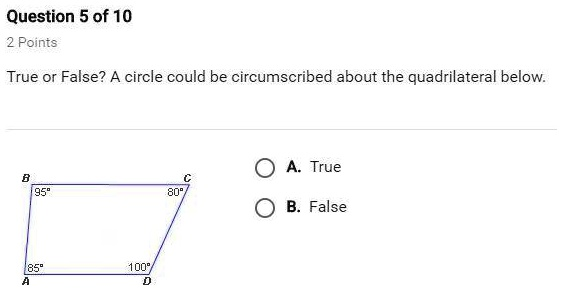
‘True or false? A circle could be circumscribed about the quadrilateral below. Question 5 of 10 2 Points True or False? A circle could be circumscribed about the quadrilateral below: True False’
The Correct Answer and Explanation is:
The statement is True, provided the quadrilateral is a cyclic quadrilateral.
A cyclic quadrilateral is one in which all four vertices lie on a single circle. This means that the quadrilateral can be circumscribed about a circle. The defining property of a cyclic quadrilateral is that the sum of the opposite angles is always 180°.
Key Conditions for a Circle to Be Circumscribed Around a Quadrilateral:
- Opposite Angles Add Up to 180°: In any cyclic quadrilateral, the sum of opposite angles is 180°. This is a fundamental theorem of cyclic quadrilaterals, often referred to as the cyclic quadrilateral angle theorem.
- Circumscribed Circle: A circle that passes through all four vertices of the quadrilateral is called the circumscribed circle. This circle’s center is equidistant from the vertices of the quadrilateral.
- Ptolemy’s Theorem: For a quadrilateral to be cyclic, Ptolemy’s Theorem must hold, which states that the product of the diagonals of the quadrilateral is equal to the sum of the products of opposite sides.
Example of Cyclic Quadrilateral:
A square or rectangle is an example of a cyclic quadrilateral, as all of their vertices lie on the circumference of a circle. Other quadrilaterals, such as trapezoids or general irregular quadrilaterals, may or may not be cyclic.
Conclusion:
If the quadrilateral in question satisfies the properties mentioned above, such as having opposite angles summing to 180° or fulfilling Ptolemy’s Theorem, then it is cyclic, and a circle can be circumscribed about it. If not, it is non-cyclic, and no circle can be drawn around it.
