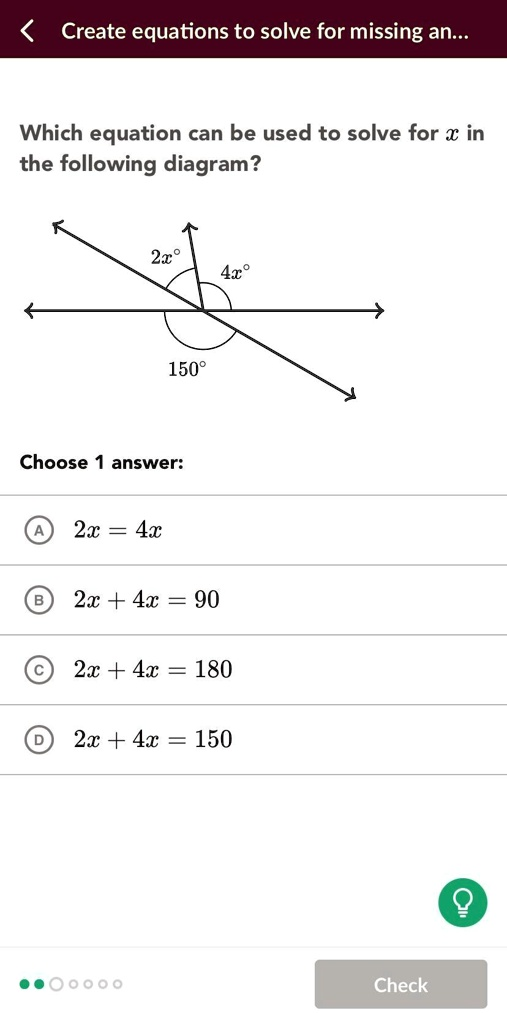
Which equation can be used to solve for x in the following diagram

Which equation can be used to solve for x in the following diagram? Choose 1 answer. 2x° degrees, 4x° degrees, 150° degrees Create equations to solve for missing angle. Which equation can be used to solve for x in the following diagram? 2x 4x 150 Choose answer: 2x 4x 2x + 4x = 90 2x + 4x = 180 2x + 4x = 150 Check

The Correct Answer and Explanation is:

The correct answer is D) 2x + 4x = 150.

Here is a detailed explanation of how to arrive at this equation:

The problem requires identifying the correct equation to solve for the variable x in the given diagram. To do this, we need to use fundamental principles of geometry related to intersecting lines and angles.

The key concept for solving this problem is the property of vertical angles. When two straight lines intersect, they form pairs of opposite angles. These opposite angles are called vertical angles, and they are always equal to each other.

In the provided diagram, we can see two main lines intersecting: a horizontal line and a slanted line. This intersection creates four angles.

1. One of the angles formed by this intersection is explicitly labeled with a measure of 150°. This angle is located below the horizontal line.
2. The angle that is directly opposite to the 150° angle across the intersection point is its vertical angle. According to the rule of vertical angles, this opposite angle must also have a measure of 150°.
3. If we look at the diagram, this vertical angle (located above the horizontal line) is shown to be composed of two smaller, adjacent angles. The measures of these two smaller angles are given in terms of x: 2x° and 4x°.
4. The total measure of this composite angle is the sum of its two parts. Therefore, the total measure of the angle vertically opposite to the 150° angle is (2x + 4x)°.
5. Since the two vertical angles are equal, we can set their measures equal to each other. This gives us the equation:2x + 4x = 150

This equation correctly represents the relationship between the angles in the diagram and can be used to solve for x. This matches option D.