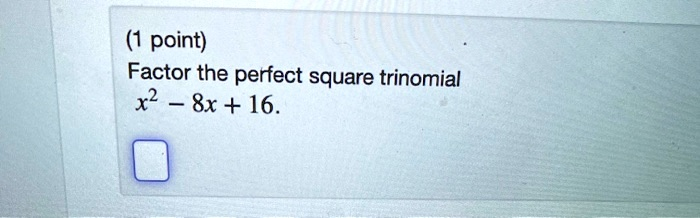
point) Factor the perfect square trinomial x2 8x + 16.
The Correct Answer and Explanation is:
The correct factored form of the perfect square trinomial x² – 8x + 16 is (x – 4)².
Explanation
A perfect square trinomial is a specific type of quadratic expression that is the result of squaring a binomial. There are two standard patterns to recognize for perfect square trinomials:
- a² + 2ab + b² = (a + b)²
- a² – 2ab + b² = (a – b)²
To factor the given expression, x² – 8x + 16, we need to determine if it fits one of these patterns.
Step 1: Identify the ‘a’ and ‘b’ terms.
First, we look at the first and last terms of the trinomial to see if they are perfect squares.
The first term is x². This is the square of x. So, we can set a = x.
The last term is 16. This is the square of 4. So, we can set b = 4.
Step 2: Check the middle term.
Now, we must verify if the middle term, -8x, matches the pattern. Since the middle term is negative, we should check it against the second formula’s middle term, which is -2ab.
Let’s substitute our values of ‘a’ and ‘b’ into this formula:
-2ab = -2 * (x) * (4) = -8x
The result, -8x, is exactly the same as the middle term in our original expression. This confirms that the trinomial x² – 8x + 16 is a perfect square and fits the pattern a² – 2ab + b².
Step 3: Write the factored form.
Since the trinomial matches the pattern a² – 2ab + b², its factored form is (a – b)². We can now substitute our values for ‘a’ and ‘b’ into this factored form:
(a – b)² = (x – 4)²
To double check the answer, you can expand (x – 4)²:
(x – 4)(x – 4) = x² – 4x – 4x + 16 = x² – 8x + 16.
This matches the original expression, confirming our factorization is correct.
