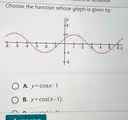
The Correct Answer and Explanation is:
Expand to view model thoughtschevron_right
The correct function for the given graph is y = cos(x).
To determine the correct function, we can analyze the key features of the graph: its amplitude, period, vertical shift, and phase shift.
First, let’s identify the amplitude and vertical shift. The graph reaches a maximum height of y = 1 and a minimum height of y = -1. The midline of the graph is the horizontal line halfway between the maximum and minimum values. We can calculate this as (1 + (-1)) / 2 = 0. Therefore, the midline is the x-axis, or y = 0. This indicates that there is no vertical shift up or down. The amplitude is the distance from the midline to either the maximum or minimum point. In this case, the amplitude is 1 – 0 = 1.
Next, we examine the period and phase shift. The period is the length of one complete cycle of the wave. The graph shows a peak at x = 0. Following the curve, it completes one full cycle and reaches the next peak at approximately x = 6.28. This value is equivalent to 2π, which is the standard period for the parent cosine and sine functions. The phase shift refers to the horizontal translation of the graph. The basic function y = cos(x) is known to have a peak at x = 0. Since the given graph also has a peak at x = 0, there is no horizontal or phase shift.
Based on this analysis, the graph has an amplitude of 1, a midline of y = 0 (no vertical shift), a period of 2π, and no phase shift. These characteristics perfectly describe the parent function y = cos(x).
Now, we can evaluate the visible options to confirm our conclusion.
Option A, y = cos(x) – 1, represents a cosine function shifted down by one unit. Its midline would be y = -1, and its range would be from 0 to -2. This does not match the graph.
Option B, y = cos(x – 1), represents a cosine function shifted to the right by one unit. Its peak would occur at x = 1, not at x = 0. This also contradicts the given graph.
Thus, the graph shown is a perfect representation of the function y = cos(x).
