The Correct Answer and Explanation is:
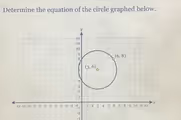
The correct equation for the circle graphed is (x – 3)² + (y – 4)² = 25.
To find the equation for the circle shown, we use the standard form for a circle’s equation: (x – h)² + (y – k)² = r². In this general formula, the point (h, k) represents the coordinates of the circle’s center, and the variable r stands for the length of its radius. Our goal is to determine the specific values for h, k, and r based on the information provided in the graph.
First, we identify the center of the circle, (h, k). The graph clearly marks the center with its coordinates. By reading the graph, we can see the center is located at the point (3, 4). This gives us the values for h and k to use in our equation. The x-coordinate of the center is h, so h = 3, and the y-coordinate is k, so k = 4.
Next, we must calculate the radius, r. The radius is the distance from the center of the circle to any point on its circumference. The graph helpfully provides another labeled point that lies on the circle itself, which is (6, 8). We can determine the length of the radius by calculating the distance between the center (3, 4) and this point (6, 8). For this calculation, we apply the distance formula: r = √[(x₂ – x₁)² + (y₂ – y₁)²].
By substituting the coordinates of the center and the point on the circle into this formula, we get the following calculation:
r = √[(6 – 3)² + (8 – 4)²]
r = √[(3)² + (4)²]
r = √[9 + 16]
r = √25
This result shows that the radius of the circle is 5 units.
Finally, we can construct the specific equation for the circle by substituting the values we found for h, k, and r into the standard formula. With h = 3, k = 4, and r = 5, the equation is:
(x – 3)² + (y – 4)² = 5²
The last step is to square the radius. This gives us the final equation for the circle: (x – 3)² + (y – 4)² = 25.
