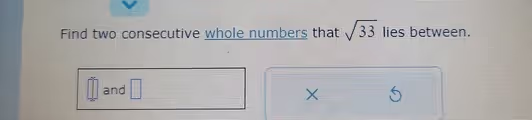
The Correct Answer and Explanation is:
The correct answer is 5 and 6.
To determine which two consecutive whole numbers the square root of 33 lies between, we need to find the perfect squares that are immediately below and above 33. A whole number is a non negative integer like 0, 1, 2, 3, and so on. Consecutive whole numbers are numbers that follow each other in order, such as 4 and 5 or 10 and 11. A perfect square is the result of multiplying a whole number by itself.
Let’s begin by listing some perfect squares to identify where 33 would fit:
1² = 1 x 1 = 1
2² = 2 x 2 = 4
3² = 3 x 3 = 9
4² = 4 x 4 = 16
5² = 5 x 5 = 25
6² = 6 x 6 = 36
7² = 7 x 7 = 49
From this list, we can observe that the number 33 is greater than the perfect square 25 and less than the perfect square 36. This relationship can be expressed using an inequality:
25 < 33 < 36
Because all the numbers in this inequality are positive, we can take the square root of each part without changing the direction of the inequality signs. This gives us a new inequality:
√25 < √33 < √36
Next, we calculate the square roots of the perfect squares. The square root of 25 is 5, since 5 times 5 is 25. The square root of 36 is 6, since 6 times 6 is 36.
By substituting these values back into our inequality, we get the final result:
5 < √33 < 6
This inequality clearly shows that the value of the square root of 33 is a number that is larger than 5 but smaller than 6. Therefore, the two consecutive whole numbers that the square root of 33 lies between are 5 and 6. This method provides a straightforward way to estimate the value of an irrational square root by placing it between two known integers.
